Sample Math Programs
These sample math programs are REALLY simple examples of using programming to solve math problems. L. Prevett, a Mathematics Instructor at Cochise College in Sierra Vista Arizona (US) posted a request on the seul-edu mailing list ( http://www.seul.org/edu/ ) asking for program examples. He writes I think the reason I can't find anything like this is that it is TOO simple.
Each program should be a complete sample script. Linux users should be able to save the code to a file, then use the command tclsh filename to run the program. (Note that Linux users might have to type tclsh<TAB> to get a particular version of tclsh, like tclsh8.0.)
Here is a list of simple programs that he would like to see. Can you help write one of them? I think the goal is to show how to use a programming language to solve a problem, as opposed to a demonstration of efficient algorithms, so don't worry too much about tuning for optimum performance.
- A program that does a loop and prints the numbers from 1 to 10
- A program that sums the numbers in a list (NEW), mean, square mean, standard deviation
- A program that factors a number
- A program that generates a list of prime numbers and prints the results to a file
- A program that reads a list of numbers from a file and prints their factors
- A program that uses the Euclidean Algorithm to print the gcd of two numbers
- A program that computes a factorial using recursion
- A program that prints an addition table
- A program that prints a multiplication table
- A program that prints a multiplication table mod n
- A program that prints the sum of two squares
- A program that inputs b,n, and p and prints b^n mod p for n=1 to n-1
- A program that prints the sum of the numbers from 1 to n.
- A program that computes the 'osculator' for a prime number and uses it to test an input number for divisibility by that prime.
- Fraction math has some related programs.
- A program that inputs a number and a counting interval and prints the Ring of Josephus.
- A program that prints the partitions of a number.
- A program to approximate pi using Monte-Carlo methods.
- A simple calculator (mathematically oriented input or remembered functions?)
- A program that computes 1000 digits of e using a spigot algorithm.
Any others?
RWT
---
For dealing with complex numbers see Complex math made simple.
---
After conferring with RWT I put these programs along with most of the comments in the K-12 Mathematics Teachers Guide for Linux [L1 ] being developed for SEUL. The programs are in the "Programming Mathematics" [L2 ] section under "tcl/tk" [L3 ]. There is also a link to "Suggested Programming Problems for Mathematics" [L4 ] on that page.
Thanks to all the members of the comp.lang.tcl newsgroup and the Tcler's Wiki who have contributed programs. If I didn't get some of the credits right, or if I missed a credit, or if you have any comments or other issues, please feel free to contact me.
L. Prevett, Mathematics Instructor Cochise College, Sierra Vista, AZ, US [email protected], 11-2-00
LV I was wondering today whether the original requestor was interested in examples that demonstrate how one can make use of fancy tcl tricks to get the fastest answers, examples that demonstrate the underlying mathematical concepts, or just examples of any code that provides the reader with answers (and who cares how or why the program works)?
A program that does a loop and prints the numbers from 1 to 10
# A program that does a loop and prints
# the numbers from 1 to 10
#
set n 10
for {set i 1} {$i <= $n} {incr i} {
puts $i
}or alternatively
# A program that does a loop and prints
# the numbers from 1 to 10
#
set i 1
while {$i <= 10} {
puts $i
incr i
}These are just like in C. Another, Tcl-only alternative for short lists:
foreach i {1 2 3 4 5 6 7 8 9 10} {puts $i} ;#RSA program that sums the numbers in a list
proc lsum L {expr [join $L +]+0}This brief little beauty does no I/O (which should be separated anyway). In an interactive tclsh, the last result is automatically output. So you can test it with
lsum {1 2 3 4.5}
% 10.5This very Tcl'ish style concatenates the elements of L with a plus sign, which then looks like 1+2+3+4.5, appends +0 to the end (just in case the list was empty) and has the resulting string evaluated by expr (and as DKF measured, this is pretty efficient - see Lambda in Tcl). As the expr is the (first, only, and) last command in the proc, an explicit return is not needed. Again for conciseness, a one-element arg list for proc need not be braced. While we're at it, the arithmetic average can be done with
proc lavg L {expr ([join $L +])/[llength $L].}We don't have to provide for empty lists here, since we can't divide by a length of 0... See Steps towards functional programming on how to use this in powerful one-liners. - As I just needed them, here's square mean and standard deviation also:
proc mean2 list {
set sum 0
foreach i $list {set sum [expr {$sum+$i*$i}]}
expr {double($sum)/[llength $list]}
}
proc stddev list {
set m [lavg $list]
expr {sqrt([mean2 $list]-$m*$m)}
} ;# RS# mad - I tried the above lsum implementation with large lists having elements in excess of 30,000. It gets very slow and results in segmentation fault. So, take a judgement on based on your use case.
A program that factors a number
# A program that factors a number
puts -nonewline "Enter number to factor: "
set num [gets stdin]
for {set i $num} {$i>0} {incr i -1} {
if { $num % $i == 0 } {
puts $i
}
}MS: I understand "factor a number" as "producing the list of prime factors"; the algorithm above produces instead a list of all integer divisors (after cleaning up the syntax ...)
So, I propose instead:
# A program that factors a number
proc factor_num {num} {
for {set i 2} {$i <= $num} {} {
if {![expr {$num % $i}]} {
lappend factors $i
set num [expr {$num / $i}]
} else {
incr i
}
}
return $factors
}
proc factor_run {} {
puts -nonewline "Enter number to factor: "
flush stdout
set num [gets stdin]
if { [expr {int(abs($num))}] != $num } {
puts "Sorry: only non-negative integers allowed"
} else {
set factors [factor_num $num]
puts "$num = [join $factors { * }]"
}
}
factor_run
# end of programMore efficient for large numbers would be
proc factor_num {num} {
for {set i 2} {$i <= $num} {} {
if {![expr {$num % $i}]} {
lappend factors $i
set num [expr {$num / $i}]
} elseif {[expr $i*$i > $num]} {
lappend factors $num
break
} elseif {$i != 2} {
incr i 2
} else {
set i 3
}
}
return $factors
}'italic text'**A program that generates a list of prime numbers and prints the results to a file**
proc all_primes {max} {
set primes [list 2]
for {set test 3} {$test <= $max} {incr test 2} {
set maxTest [expr {int(sqrt($test))}]
foreach prime $primes {
if {$prime > $maxTest} {
lappend primes $test
break
}
if {![expr {$test % $prime}]} {
break
}
}
}
return $primes
}
proc all_primes_run {} {
puts -nonewline "Compute all primes below: "
flush stdout
set max [gets stdin]
if {$max < 2} {
set max 2
}
set primes [all_primes $max]
set f [open "primes_below_$max" w]
puts $f $primes
close $f
}
all_primes_run
# end of programA program that reads a list of numbers from a file and prints their factors.
# Start by including one of the factor_num procedures
# defined above, then just read a file print the factors.
set f [open "test.dat" r]
while { ! [eof $f] } {
scan [gets $f] %i number
set factors [factor_num $number]
puts "$number: $factors"
}
close $fA program that uses the Euclidean Algorithm to print the GCD (greatest common divisor) of two numbers
proc gcd {num1 num2} {
while {[set tmp [expr {$num1%$num2}]]} {
set num1 $num2
set num2 $tmp
}
return $num2
}A program that computes a factorial using recursion*
proc fact {num} {
if {$num} {
return [expr {$num * [fact [incr num -1]]}]
} else {
return 1
}
}
proc fact_run {} {
puts -nonewline "Compute the factorial of: "
flush stdout
set num [gets stdin]
if { [expr {int(abs($num))}] != $num } {
puts "Sorry: only non-negative integers allowed"
} else {
puts [fact $num]
}
}
fact_runDKF - It is more efficient to use iteration:
proc fact {n} {
set f 1
for {set i 1} {$i<=$n} {incr i} {
set f [expr {$f * $i}]
}
return $f
}A program that prints some mathematical operation tables!
proc table { op N } {
set table "$op table\n"
for { set i 1 } { $i <= $N } { incr i } {
lappend line $i
}
set i 0
set magic {}
switch -exact -- $op {
+ { set i -2 }
/ { set magic .0 }
}
while { [ incr i ] <= $N } {
foreach item $line {
append table " [ expr $item$op$i$magic ]"
}
append table "\n"
}
set table
}
foreach op { * + / - == != > >= < <= } {
puts [ table $op 10 ]
}-PSE
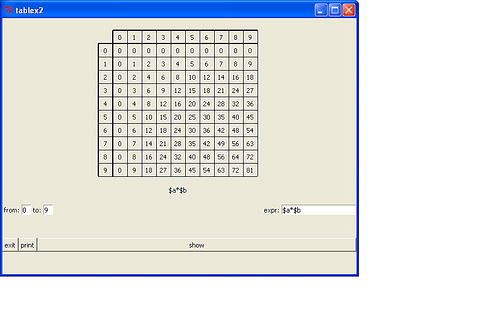
A program displaying any expression table (wish version)
# a program displaying any expression table (FP)
set first 0
set last 9
set expr {$a+$b}
# can be replaced interactively by {$a*$b}, {($a*$b)%7)}, ...
set LP lp ;# machine dependent print command
proc showTable {first last oper} {
set terms [list]
for {set i $first} {$i <= $last} {incr i} {
lappend terms $i
}
set n [llength $terms]
set hdx 12
set hdy 11
set bx 20
set by 20
.c delete all
.c configure -width [expr {2*($n+1)*$hdx + 2*$bx}] -height [expr {(2*$n+4)*$hdy + 2*$by}]
set ia 0
foreach a $terms {
incr ia
set ib 0
foreach b $terms {
incr ib
set r [expr $oper]
.c create text [expr {(2*$ib+1)*$hdx + $bx}] [expr {(2*$ia+1)*$hdy + $by}] -text $r
}
}
.c create text [expr {($n+1)*$hdx + $bx}] [expr {(2*$n+4)*$hdy + $by}] -text $oper
set ia 0
foreach a $terms {
incr ia
.c create text [expr {(2*$ia+1)*$hdx + $bx}] [expr {$by + $hdy}] -text $a
.c create text [expr {$bx + $hdx}] [expr {(2*$ia+1)*$hdy + $by}] -text $a
.c create line\
[expr {$bx}] [expr {$by + (2*$ia+2)*$hdy}]\
[expr {$bx + (2*$n + 2)*$hdx}] [expr {$by + (2*$ia+2)*$hdy}]
.c create line\
[expr {$bx + (2*$ia+2)*$hdx}] [expr {$by}]\
[expr {$bx + (2*$ia+2)*$hdx}] [expr {$bx + (2*$n+2)*$hdy}]
}
.c create line\
[expr {$bx + 2*$hdx}] [expr {$by}]\
[expr {$bx + (2*$n+2)*$hdx}] [expr {$by}] -width 2
.c create line\
[expr {$bx}] [expr {$by + 2*$hdy}]\
[expr {$bx}] [expr {$bx + (2*$n+2)*$hdy}] -width 2
.c create line\
[expr {$bx}] [expr {$by + 2*$hdy}]\
[expr {$bx + (2*$n+2)*$hdx}] [expr {$by + 2*$hdy}] -width 2
.c create line\
[expr {$bx + 2*$hdx}] [expr {$by}]\
[expr {$bx + 2*$hdx}] [expr {$bx + (2*$n+2)*$hdy}] -width 2
}
canvas .c
pack .c
frame .f
label .f.l1 -text from:
label .f.l2 -text to:
entry .f.e1 -textvariable first -width 2
entry .f.e2 -textvariable last -width 2
label .f.l3 -text {expr:}
entry .f.e3 -textvariable expr
pack .f.l1 .f.e1 .f.l2 .f.e2 -side left
pack .f.e3 .f.l3 -side right
pack .f -fill x
button .bp -text print -command {exec $LP << [.c postscript]}
button .bq -text exit -command exit
pack .bq .bp -side left
button .b -text show -command {showTable $first $last $expr}
pack .b -side right -expand y -fill x
.b invoke
# end of programA program that prints a multiplication table
# A program to print a multiplication table to the screen
proc times_table { x } {
puts "Multiplication table for $x."
for {set i 1 } { $i < 10} {incr i } {
set answer [expr $x * $i]
puts "$x times $i = $answer"
}
}
proc run_table { } {
puts -nonewline "Enter a number: "
flush stdout
set x [gets stdin]
times_table $x
}
run_table
#end of programA program that prints a multiplication table mod n
I noticed that the 'any expression' table script above will print a multiplication (or addition, etc) table mod n.
For example,
from: 1 to: 4 expr: ($a * $b) % 5
prints the multiplication table mod 5.
By the way, these scripts are really great!
lp
A program that prints the sum of two squares
proc sum_of_two_squares { x y } {
set answer [expr $x*$x + $y*$y]
puts $answer
}so
A program that inputs b,n, and p and prints b^n mod p for n=1 to n-1
KBK (4 Oct 2000):
proc modular_exponent_table { b p } {
set value 1
for {set n 1} {$n < $p} {incr n} {
set value [expr {($value * $b) % $p}]
puts "( $b ** $n ) mod $p == $value"
}
};# edited for clarity and style by DKF
puts -nonewline stdout "Enter base b: "
flush stdout
gets stdin b
puts -nonewline stdout "Enter modulus p: "
flush stdout
gets stdin p
modular_exponent_table $b $pRunning the above gives:
% tclsh83 prime_power.tcl Enter base b: 3 Enter modulus p: 17 ( 3 ** 1 ) mod 17 == 3 ( 3 ** 2 ) mod 17 == 9 ( 3 ** 3 ) mod 17 == 10 ( 3 ** 4 ) mod 17 == 13 ( 3 ** 5 ) mod 17 == 5 ( 3 ** 6 ) mod 17 == 15 ( 3 ** 7 ) mod 17 == 11 ( 3 ** 8 ) mod 17 == 16 ( 3 ** 9 ) mod 17 == 14 ( 3 ** 10 ) mod 17 == 8 ( 3 ** 11 ) mod 17 == 7 ( 3 ** 12 ) mod 17 == 4 ( 3 ** 13 ) mod 17 == 12 ( 3 ** 14 ) mod 17 == 2 ( 3 ** 15 ) mod 17 == 6 ( 3 ** 16 ) mod 17 == 1
KBK (10 Oct 2000): I'm not sure that I like the change that DKF made. Let's follow this up a little bit on Tcl style discussion.
A program that computes the sum of the numbers from 1 to n
# A program to compute the sum of the numbers from 1 to n
proc sumto {n} {
set sum 0
set i 1
while {$i <= $n} {
set sum [expr $sum + $i]
incr i
}
puts "The sum of the numbers from 1 to $n is $sum "
}
puts -nonewline stdout "Enter a number: "
flush stdout
gets stdin n
sumto $n
# end of program
# I'm no programmer, but I wanted to see if I could use the examples
# on this page to write this program. I think it works ...lp
Minor style note - It is better to use the [for] command for the style of loop you were doing above as it is easier to understand the purpose of the loop when you come back to look at it later; code has this way of lasting far longer than you intended... DKF
RS -- Also, a proc should return the result rather than puts'ing it. So here's my version:
proc sumto n {
set sum 0
for { set i 1 } { $i <= $n } { incr i } {
incr sum $i
}
return $sum
}KBK -- I edited this (18 October 2000) to spare Donal's tender sensibilities (see Tcl style discussion).
JCE - so why not just this:
proc sumto n {
expr $n * ($n + 1) / 2
}A program that computes the osculator for a prime number, and uses it to test an input number for divisibility by that prime
# I thought the group might be interested in this problem. # This would be a more challenging program for students to # program because they have to access individual digits in # numbers to form new numbers. # Numbers that end in even numbers or 5 are easy to factor. # Numbers that end in 1,3,7,9 are generally more difficult. # Divisibility tests exist for numbers that end in # 1,3,7, or 9, but they use a special 'osculator'. # For example, the osculator for 7 is 5. To test 343 for # divisibility by 7, here's what you do: # multiply the rightmost digit by the osculator, 5: 3x5 = 15 # add the result to all the digits to the left of 3: 34 + 15 = 49 # since 49 is divisible by 7, 343 will be divisible by 7. # To compute the osculator for any number, first multiply # by (the smallest) number that gives a product whose rightmost # digit is '9'. Drop the '9' and add 1 to all the remaining digits. # The osculator for 71 is 64: 71 x 9 = 639, 63 + 1 = 64. # The osculator for 23 is 7: 23 x 3 = 69, 6 + 1 = 7. # The osculator for 17 is 12: 17 x 7 = 119, 11 + 1 = 12. # The osculator for 19 is 2: 19 x 1 = 19, 1 + 1 = 2. # Another example. Is 3534 divisible by 19? # The osculator for 19 is 2. # 4 x 2 = 8, 353 + 8 = 361 # 1 x 2 = 2, 36 + 2 = 38 # Since 38 is divisible by 19, 3534 is divisible by 19. # Incidentally, if the sum of the digits of a number sum to '3' # then the number itself is divisible by 3. This is because the # osculator for 3 is '1': 3 x 3 = 09, 0 + 1 = 1.
lp
You do not really need to access individual digits: just the last one, and the rest. This can be done simply by dividing by 10 (modular or integer division). For instance, to compute the osculator of any number, just do:
proc osc {base} {
for {set i 1} {1} {incr i} {
set tmp [expr {$base * $i}]
if [expr {($tmp % 10) == 9}] {
return [expr {($tmp / 10) + 1}]
}
}
}A safer version is
array set mult [list 1 9 3 3 7 7 9 1]
proc osc {base} {
global mult
set last [expr {$base % 10}]
if {[catch {set coeff $mult($last)}]} {
return "Only valid for numbers ending in 1, 3, 7 or 9 ..."
} else {
return [expr {(($base * $coeff) / 10) + 1}]
}
}MS
DKF - We can leverage Tcl's string/number duality capabilities to help here. Note, there's not many other languages where you'd solve the problem like this...
proc osc base {
if {[regexp {[1379]$} $base digit]} {
set coeff [lindex {? 9 ? 3 ? ? ? 7 ? 1} $digit]
return [expr {($base * $coeff / 10) + 1}]
}
return -code error "base must end in 1, 3, 7 or 9 ..."
}lp - So, here's a mangled attempt at a divisbility test using one of the three 'osc' procs above.
# perform one osculation of n by m
proc oscit {n m} {
set adder [expr {$m*($n % 10)}]
set left_digits [expr {int($n / 10)}]
return [expr {$left_digits + $adder}]
}
# Test the divisibilty of num by prime.
# use a maximum of 9 digits for the number
# 123456789
set num 211111043
set prime 23
# get the osculator for the prime
set osc_p [osc [expr $prime]]
# get the number of digits in the number
# will osculate the number this many times
set n_digits [string length $num]
# compute and print osculations
set x $num
for {set j 1 } { $j < $n_digits} {incr j } {
puts -nonewline "$x, "
# proper way to call oscit with 2 vars?
set x [oscit [expr $x] [expr $osc_p]]
}
puts "$x ..."
# print the results
puts "$n_digits osculations of $num by osculator $osc_p for prime $prime."
if [expr !($x % $prime)] {
puts "Since $x is divisible by $prime, $num is divisible by $prime."
} else {
puts "Since $x is not divisible by $prime, $num is not divisible by $prime."
# A note for the 'else' case ...
# The following is an example of the kinds of patterns that can be
# noticed in mathematics with the use of a computer. Such patterns
# often lead to new insights, new proofs, new theorems, etc.
puts "Conjecture: continued osculation produces a list of numbers\
with period $prime - 1 = [expr $prime - 1]:"
for {set j 1 } { $j < $prime } {incr j } {
puts -nonewline "$x, "
set x [oscit [expr $x] [expr $osc_p]]
}
puts "$x ..."
puts "Conjecture: It appears that each number in the first half\
added to its conjugate in the second half is divisible by $prime."
}
# end programlp
A program that prints the Ring of Josephus
# For the Ring of Josephus, you start with a list of elements # from 1 to n, and a counting interval, k. # You make one pass through the list selecting each kth element # in the list. You 'delete' each element as it is selected. # You continue to select and delete each kth element until # no more elements remain. The permutation generated # describes the order in which each number has been chosen. # First selection for 7 elements and a counting interval of 4: # 1 2 3 4 5 6 7 <-- number # _ _ _ 1 _ _ _ <-- order chosen # Second selection, 7 elements and a counting interval of 4: # 1 2 3 4 5 6 7 <-- number # 2 _ _ 1 _ _ _ <-- order chosen # etc. # For 7 elements and a counting interval of 4: # 1 2 3 4 5 6 7 <-- number # 2 7 6 1 4 3 5 <-- order chosen # For 13 elements and a counting interval of 3: # 1 2 3 4 5 6 7 8 9 10 11 12 13 # 11 5 1 8 10 2 6 12 3 9 7 4 13 # This is called the Ring of Josephus because, as one version of # the story goes, around 63 A.D. 13 soldiers formed a suicide pact # instead of surrendering to the Romans. They stood in a circle and # counted around by 3's killing each man in turn. The final man # standing was to commit suicide. Their leader, Josephus, had # cleverly chosen his position to be 'last'. Along with his best # friend who was in the 'next to last' position, they deserted # to the Roman army. # I'm told that there are applications in coding theory and # networking, but I've never found anything on the web. # I use this as an example of a problem that cannot be solved # algebraically. Except for a few special cases there is no # known formula that will predict when an element will be # chosen for an arbitrary number of elements and counting interval. # The answer must be determined by construction (programming.)
lp
# Program to generate Ring of Josephus by DKF
proc ROJ {{n 13} {skip 3}} {
set list {}
set result {}
for {set i 1} {$i<=$n} {incr i} {
lappend list $i
}
set i 0
while {[llength $list]} {
set i [expr {($i+$skip)%[llength $list]}]
lappend result [lindex $list $i]
set list [lreplace $list $i $i]
}
return $result
}
proc PrintRingOfJosephus {ringSize skipNumber} {
for {set i 1} {$i<=$ringSize} {incr i} {
puts -nonewline [format %4d $i]
}
puts ""
foreach i [ROJ $ringSize $skipNumber] {
puts -nonewline [format %4d $i]
}
puts ""
}A program that prints the partitions of a number
# The partitions of a number are simply the different ways a # number can be summed. (Summands are in descending order.) # There are 7 partitions of 5: 5, 41, 32, 311, 221, 2111, 11111 # There are 14 partitions of 7: # 7, 61, 52, 511, 43, 421, 4111, 322, 3211, # 3111, 2221, 22111, 211111, 1111111 # The number of partitions becomes large very quickly. Although # simple, partitions are of theoretical interest in number # theory and physics.
lp
KBK (17 October 2000): Here's one possibility:
#----------------------------------------------------------------------
#
# part --
#
# List the partitions of a number, optionally limiting the size
# of the largest element.
#
# Parameters:
# n -- Number to be partitioned
# k -- (Optional) Size of the largest element. Default is n.
#
# Results:
# Returns a list of the partitions of n with no element larger
# than k, in reverse lexicographic order.
#
# Side effects:
# None.
#
#----------------------------------------------------------------------
proc part { n { k -1 } } {
# If k is not supplied, or if k is greater than n (no partition
# of n can have an element greater than n), set k to the default
# of n.
if { $k < 0 || $k > $n } {
set k $n
}
# There is only one partition of zero: the empty list.
if { $n == 0 } {
return [list [list]]
}
# Accumulate the list of partitions. This is done by choosing
# the largest element r of the partition, then partitioning
# the remaining n-r so that no element is greater than r.
set parts {}
for { set r $k } { $r > 0 } { incr r -1 } {
foreach list [part [expr { $n - $r }] $r] {
lappend parts [linsert $list 0 $r]
}
}
# Return the accumulated list.
return $parts
}
# Main program to demonstrate partitioning of integers.
for { set i 0 } { $i <= 7 } { incr i } {
puts "Partitions of $i:"
foreach list [part $i] {
puts $list
}
}A program to compute pi using Monte-Carlo methods
# x^2 + y^2 = 1 is a circle of radius 1.
# Many random coordinates for x and y are generated
# in the first quadrant of the x-y plane and tested
# to see whether the points fall inside the circle.
# The area in quad I for a unit circle is pi/4.
# The ratio of the pairs inside the circle to the
# total number of points tested approaches pi/4 when
# the number of random points is large enough.
set n 1000000
set count 0
for {set i 1} {$i <= $n} {incr i} {
set x [expr rand()]
set y [expr rand()]
if {[expr {($x*$x + $y*$y) < 1}]} {
incr count }
}
puts "Number of points inside the circle= $count"
puts "Total points = $n"
set pi [expr 4e+0*$count/$n]
puts "Approximation for pi is $pi"
# For 1,000,000 points pi is computed correct to 2 decimal places.
# Below is the result for 5 trials. My sensibilities tell me that
# the approximation should be better, and more convergent.
# Any ideas on why there is so much divergence in the results?
# Am I handling the [rand] function incorrectly?
# (Even for awk, there is 3 place decimal accuracy for n=1M.)
# Is it due to the fact that rand() uses the clock and
# does not generate 'true' random numbers?
# Should I be using srand()?
#
# Also, it was necessary to use [expr 4e+0*$count/$n]
# to get a floating point answer. [expr $count/$n] gives 3.
# There seem to be some subtleties in this simple program
# that I don't feel qualified to explain.
# Any thoughts would be appreciated.
# 5 trials for tcl/tk:
# points inside: 785907, 785725, 785062, 785194, 785041
# approx for pi: 3.143628, 3.1429, 3.140248, 3.140776, 3.140164 lp
---
Sorry to report: your sensibilities are "wrong", the method is really not that accurate!
If you compute the standard deviation of your estimate (assuming that the n points that you generate are uniformly distributed in the unit square), you obtain
s = sqrt(pi(4-pi)/n) ~ 1.64/sqrt(n)
If piE is the resulting estimate for n=1E6, this means that
- |piE - pi| < s ~ 1.64E-3 with probability 0.68
- |piE - pi| < 2s ~ 3.28E-3 with probability 0.95
- |piE - pi| < 3s ~ 4.92E-3 with probability 0.997
So: you have no right to expect better than two decimal digits accuracy with this method and a million points.
Remark that if you use 5 million points (i.e., if you average your 5 results), the resulting standard deviation goes down to
s ~ 1.64E-3/sqrt(5) ~ 7.3E-4
giving a reasonable probability of hitting the third decimal digit ...
ms
---
I bow to your lamp, sir! Thanks for the reminder to check the math before jumping to conclusions about the code.
More info on the rand function is here: rand
lp
---
DKF - Point of Tcl style:
It is better to write the above code as:
proc montecarlo-pi {n} {
set count 0
for {set i 1} {$i <= $n} {incr i} {
set x [expr {rand()}]
set y [expr {rand()}]
if {($x*$x + $y*$y) < 1} {
incr count
}
}
expr {4e0*$count/$n}
}
puts "Approximation for pi is [montecarlo-pi 1000000]"A simple calculator
Arjen Markus A simple calculator (two types) can be found at A little math language
compute first thousand digits of e
GS Here is a small program that computes 1000 digits of e using a spigot algorithm (see also e):
# 1000 digits of e with a spigot algorithm
proc e1 {} {
set f {}
set n 1000
set b [expr {10 * $n / 4}]
for {set i 0} {$i <= $b} {incr i} {lappend f 1}
incr n -1
puts -nonewline "2."
for {set j 1} {$j <= $n} {incr j} {
set q 0
for {set i $b} {$i >= 1} {incr i -1} {
set k [expr {$i + 1}]
set x [expr {[lindex $f $i]*10 + $q}]
lset f $i [expr {$x % $k}]
set q [expr {$x / $k}]
}
puts -nonewline $q
flush stdout
}
}
e1
Reference:
- A. H. J. Sale, ''The Calculation of e to Many Significant Digits'', The Computer Journal (1968) 11 (2): pp229-230 [http://comjnl.oxfordjournals.org/content/11/2/229.full.pdf+html]
- Stanley Rabinowitz, Stanley Wagon, ''A Spigot Algorithm for the Digits of Pi'', American Mathematical Monthly 102 (3), 1995, pp195–203 [http://www.mathpropress.com/stan/bibliography/spigot.pdf]extended eucleian algorithm
aleksanteri/arezey, 17th of September 2008: A 61LOC implementation of the extended Euclerian Algorithm.
proc eea {a b} {
set r 1
set x $a
set y $b
set exprs {}
while {$r != 0} {
set r [expr $x%$y]
set q [expr ($x-$r)/$y]
puts "$x/$y = $q r $r\t$x = $y*$q+$r"
set exprs [linsert $exprs 0 [list $r $x $y $q]]
if {$r == 0 && ![info exists gcd]} {
set gcd 1
}
set x $y
set y $r
if {![info exists gcd]} {
if {($x%$y) == 0} {
set gcd $y
}
}
}
set exprs [lreplace $exprs 0 0]
puts "gcd($a,$b) = $gcd"
puts "-------------"
set pn [lindex [lindex $exprs 0] 1]
set pf 1
set nn [lindex [lindex $exprs 0] 2]
set nf [lindex [lindex $exprs 0] 3]
set exprs [lreplace $exprs 0 0]
set c p
set o n
puts "$gcd = $pn*$pf - $nn*$nf"
foreach n $exprs {
if {$c eq "p"} {set c n; set o p} else {set c p; set o n}
set 0 [lindex $n 0]
set 1 [lindex $n 1]
set 2 [lindex $n 2]
set 3 [lindex $n 3]
set ${c}n $1
set ${o}f [expr $${o}f+($${c}f*$3)]
puts "$gcd = $pn*$pf - $nn*$nf"
}
}Lars H, 2008-09-18: Urgh! That's much too complicated. 11 lines and only one loop are quite sufficient:
proc xgcd {a b} {
set r0 1; set s0 0
set r1 0; set s1 1
while {$b} {
set q [expr {$a / $b}]
set b [expr {$a - $q*[set a $b]}]
set r1 [expr {$r0 - $q*[set r0 $r1]}]
set s1 [expr {$s0 - $q*[set s0 $s1]}]
}
list $a $r0 $s0
}To demonstrate as a program:
proc eea {a b} {
foreach {d r s} [xgcd $a $b] break
puts "$d = $a*$r + $b*$s"
}How it works (beyond the ordinary greatest common denominator) is that
( r0 s0 ) ( r1 s1 )
is a matrix which, when multiplied by the initial (a,b) as a column vector on the right, computes the current (a,b):
( a ) = ( r0 s0 ) ( a_initial ) ( b ) ( r1 s1 ) ( b_initial )
Since the very last a is the gcd, the first row of the matrix gives the coefficients which express it as a linear combination of the arguments. The three lines on the form
set b [expr {$a - $q*[set a $b]}]all amount to multiplying a column vector on the left by a matrix on the form
( 0 1 ) ( 1 -q )
Screenshots
gold added pix, for math expression table script above
Here are good samples of math calculators to be used to solve common math problems.