Petri Nets
We are beginning to use petri nets to model our workflows in OpenACS.
If you want to know why, this is a good place to start reading.
PS I found a nice, free Tk petri net editor/simulator here .
Christian Stehno 2004-05-19: For a good introduction on Petri nets try http://www.informatik.uni-hamburg.de/TGI/PetriNets/ (this used to be: http://www.daimi.au.dk/PetriNets/ )
You can also find the Petri net tool database there, which also features another Tcl/Tk based Petri net tool - The PEP tool. Check http://peptool.sourceforge.net/ for more information.
(Note: I updated the above link to Wil van der Aalst's homepage, since the old link did not work anymore).
PEP is a modelling and verification framework for parallel systems, providing a large number of different modelling languages and verification techniques (e.g. SDL, Petri nets and model checking), linked together within a Tcl/Tk-based graphical user interface. PEP's modelling components facilitate the design of parallel systems by parallel programs, interacting finite automata, process algebra, or high-level/low-level Petri nets.

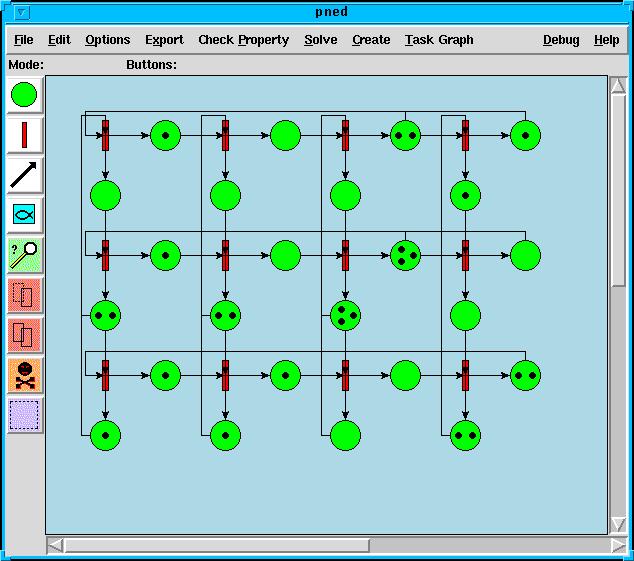
ERS is a set of tools for the analysis of discrete event systems.
ERS contains tools for
- creating graphical representations of some discrete event systems: Petri Nets, Task Graphs, Heaps of Pieces, Interaction Graphs.
- analyzing the systems and computing performance measures (throughputs and growth rates, waiting times, makespans etc.)
- transforming systems from one representation to another.
The project is a set of command-line tools written in C that can be pipelined to produce various data transformations, and/or accessed via Tcl/Tk GUI interfaces.
Roméo is a software studio for Time Petri Net analysis. It performs analysis on T-Time Petri nets and on one of their extensions to scheduling.
Roméo consists of a graphical user interface (GUI) (written in TCL/Tk) to edit and design TPNs, and of computation modules (Gpn and Mercutio, written in C++).
On Time Petri Nets, Roméo performs:
- computation of the State Space (based on State Classes or Zones)
- on-the-fly verification of properties on reachable markings
- graphical simulation of a TPN
On an extension of Time Petri Nets to scheduling (TPN with stopwatches SWPN), Roméo performs:
- computation of the State Space
- on-the-fly verification of properties on reachable markings
- graphical simulation of a TPN with stopwatches
On parametric extension of TPN and SWPN, Roméo performs:
- computation of the Parametric State Space
- on-the-fly verification of parametric properties on reachable markings
- graphical simulation
See: OPNTcl
Petrigen is a Tcl/Tk graphical Petri net editor which compiles a defined Petri net into a Prolog program, which then can be run in any Prolog environment to validate the net by treating it as a constraint solving problem.
TV: It seems suggested in that thesis (if that is what it is, I just took a quick glance) that Petri net offer some proof of correctness for executing what is called a workflow. First, correctness is even stronger than optimisation, for which one already, in the words of one of the older professors I listened to in the past, needs to know what it is that one wants to optimize!
Petri nets are mathematical stuff to define, model, simulate and to some extend reason on event driven networks of agents, which is the stronger of a few of such mathematical models because it supports multiple (parallel) firing of nodes. Which immedeately makes it the weaker or less concise candidate for accurate modeling of system behaviour composed of singularly executing units, which is the simplest and most decomposable model.
A mathematical language to do that is CSP (Hoare wrote a good book about it) or CSS (Milner) where communiction is modeled by single communication instances between agents, which are time orderable always, though not timed. The language allows composition of agents in various ways, and reasoning about strong or weak bisimularity. Which is a way of comparing possible event traces for a certain model defined by mathematical formulation of its agents and their possible communication.
For simulating event driven systems such as networks with nodes which drive eachother Petri nets allow little reasoning on the possibilities of such nets, simply because a petri net allows much to happen. When one wants to limit the behaviour of the constituing net elements, some sort of reasoning method or language with associated proof system will have to be constructed. Because n faculty is a big number, that is often hard, both to oversee and simulate.
Functional decomposition is favorite of long (at least a century) to describe complicated and connected problems, with distributiveness and substitution and such powerful means to reorder the problem into something manageable.
Christian Stehno, May 19th 2004: I don't know if I got anything correctly, but IMHO many of your above statements are wrong. First of all it is true that Petri nets allow for true concurrency semantics models. But this does not mean that they are weaker in any sense. You may as well model completely sequential systems (e.g. finite automata), and also all process algebras you mentioned (you even have Petri net algebras).
Petri nets are very powerful, but still easily comprehensible mathematical models, which have been augmented, e.g. with time annotations (to become suitable for real-time systems), rich data types (to ease the modelling part), stochastic elements (for performance evaluation) and probably every structure you can think of. There are Petri nets having programming language fragments as labels, which is to be executed during simulation and may drive Java GUI applications, you have object-oriented Petri nets, etc.
Petri nets are configurable in a large number of aspects. For your problem of "too much behavior", two ideas come up immediately. First, you may restrict behaviour by net structure, or second, you may restrict the firing rules, e.g. by disallowing multiple transitions to fire at once. But you should be aware of the fact that you will still have arbitrary interleavings of concurrent subnets, as you will have arbitrary scheduling of concurrent threads or processes on a computer. This is not a bug, but is the correct way of modelling arbitrary execution order without explicitly mentioning every possible trace. Anyway, you will definitely not need any proof system just to restrict net behavior.
Another thing one should know of Petri nets is that they build from "singularly executing units", as every transition is executing on its own, just depending on its neighbourhood. Thus, if you have two independent actions (transitions, commands, whatever), they may fire at once, but the need not. Thinking of multi-processor machines or even multithreaded processors you will even get real concurrency on your desktop, so real concurreny semantics is definitely not so artificial, and it is essential in verification of models, due to the State Explosion problem.
The task of decomposition is also known to the Petri net community, so you will find hierarchical nets, abstraction methods, reduction techniques and others, some of them even come from Petri net theory, originally.
Due to the well founded mathematics of Petri nets, fully automatic verification of models is possible. The techniques developed in this area range from simple deadlock checks to sophisticated model checking tools, which express properties in temporal logic formulae. The previously mentioned PEP tool includes a number of verification engines and analysis tools accessible via the Tcl/Tk GUI. Additionally, you may specify systems in the Specification and Description Language (SDL) of ITU-T (also part of the upcoming UML2.0), as Finite Automata, in a simple parallel programming language or in a CCS-like process algebra. All these models are then compiled into a Petri net representation in a semantics preserving way, thus analysis of the models is also possible with all available Petri net tools.