Morley's Miracle
Keith Vetter 2003-02-07 : another of the simple whizzlets, this one visualizing Morley's Miracle theorem. Just drag any vertex and watch it work.
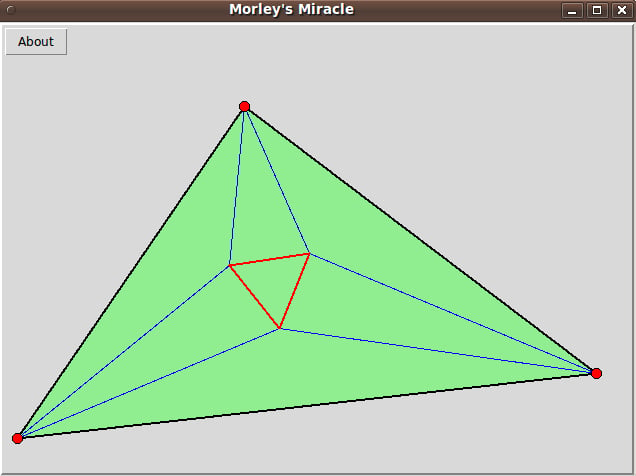
About a century ago, Frank Morley proved a curious theorem about triangles which has become known in mathematical folklore as Morley's Miracle.
The theorem states that: "The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle."
See http://www.cut-the-knot.com/triangle/Morley/Morley.shtml for more details.
#!/bin/sh -*- tab-width: 8; -*-
# The next line is executed by /bin/sh, but not tcl \
exec wish $0 ${1+"$@"}
##+##########################################################################
#
# morley.tcl -- a whizzlet visualizing Morley's Miracle
# see http://www.cut-the-knot.com/triangle/Morley/Morley.shtml
# by Keith Vetter
#
# Revisions:
# KPV Feb 07, 2003 - initial revision
#
#############################################################################
package require Tk
array set P {1 {200 50} 2 {76 381} 3 {472 309}} ;# Initial position
proc DoDisplay {} {
global P
wm title . "Morley's Miracle"
canvas .c -width 500 -height 500 -bd 2 -relief raised
pack .c -side top -fill both -expand 1
button .about -text About -command About
.c create window 5 5 -window .about -anchor nw -tag about
foreach w {1 2 3} {
.c create oval [Box $P($w)] -tag [list vert p$w] -fill red
.c bind p$w <B1-Motion> [list DoButton $w %x %y]
}
bind all <Alt-c> [list console show]
}
##+##########################################################################
#
# DoButton -- interactively moves a vertex around and redraws everything
#
proc DoButton {who X Y} {
if {$X > [winfo width .c] - 5 || $Y > [winfo height .c] - 5} return
lassign $::P($who) x y
set ::P($who) [list $X $Y]
.c move p$who [expr {$X - $x}] [expr {$Y - $y}]
DrawLines
}
##+##########################################################################
#
# Box -- returns coordinates for a box around a given point
#
proc Box {xy} {
lassign $xy x y
return [list [expr {$x-5}] [expr {$y-5}] [expr {$x+5}] [expr {$y+5}]]
}
##+##########################################################################
#
# VAdd -- adds two vectors w/ scaling of 2nd vector
#
proc VAdd {v1 v2 {scaling 1}} {
lassign $v1 x1 y1
lassign $v2 x2 y2
return [list [expr {$x1 + $scaling*$x2}] [expr {$y1 + $scaling*$y2}]]
}
##+##########################################################################
#
# VSub -- subtract two vectors
#
proc VSub {v1 v2} { return [VAdd $v1 $v2 -1] }
##+##########################################################################
#
# DrawLines -- draws all the various lines on the screen
#
proc DrawLines {} {
global P
.c delete outer tri equi
.c create poly [concat $P(1) $P(2) $P(3)] -tag outer -width 2 -fill lightgreen -outline black
DrawTrisectors
.c raise vert
}
##+##########################################################################
#
# DrawTrisectors -- draws the angle trisectors out to where they
# meet and then draws the Morley triangle in the middle.
#
proc DrawTrisectors {} {
global P
# Get trisector lines out of each vertex
lassign [TrisectAngle $P(3) $P(1) $P(2)] t(1,1) t(1,2)
lassign [TrisectAngle $P(1) $P(2) $P(3)] t(2,1) t(2,2)
lassign [TrisectAngle $P(2) $P(3) $P(1)] t(3,1) t(3,2)
# Find where trisector line segments intersect
set E1 [Intersect $P(1) $t(1,1) $P(2) $t(2,2)]
set E2 [Intersect $P(2) $t(2,1) $P(3) $t(3,2)]
set E3 [Intersect $P(1) $t(1,2) $P(3) $t(3,1)]
if {$E1 == {} || $E2 == {} || $E3 == {}} return ;# Colinear lines?
.c create line [concat $P(1) $E1 $P(2) $E2 $P(3) $E3 $P(1)] -tag tri \
-fill blue
.c create line [concat $E1 $E2 $E3 $E1] -tag equi -fill red -width 2
}
##+##########################################################################
#
# Intersect -- find where two line intersect given two points on each line
#
proc Intersect {p1 p2 p3 p4} {
lassign $p1 x1 y1
lassign $p2 x2 y2
lassign $p3 x3 y3
lassign $p4 x4 y4
set numer [expr {($x4 - $x3)*($y1 - $y3) - ($y4 - $y3)*($x1 - $x3)}]
set denom [expr {($y4 - $y3)*($x2 - $x1) - ($x4 - $x3)*($y2 - $y1)}]
if {$denom == 0} return
set X [expr {$x1 + ($numer / $denom) * ($x2 - $x1)}]
set Y [expr {$y1 + ($numer / $denom) * ($y2 - $y1)}]
return [list $X $Y]
}
##+##########################################################################
#
# TrisectAngle -- returns two points which are on the two lines trisecting
# the angle created by points p1,p2,p3. We use the cross product to tell
# us clockwise ordering.
#
proc TrisectAngle {p1 p2 p3} {
set cross [Cross [VSub $p2 $p1] [VSub $p2 $p3]]
if {$cross < 0} {lassign [list $p3 $p1] p1 p3}
set theta [FindAngle3 $p1 $p2 $p3] ;# What the angle is
set theta1 [expr {$theta / 3.0}] ;# 1/3 of that angle
set theta2 [expr {2 * $theta1}] ;# 2/3 of that angle
set v [VSub $p3 $p2] ;# We'll rotate this leg
set v1 [RotateCC $v $theta1] ;# By 1/3
set v2 [RotateCC $v $theta2] ;# By 2/3
set t1 [VAdd $p2 $v1] ;# Trisect point 1
set t2 [VAdd $p2 $v2] ;# Trisect point 2
if {$cross < 0} { lassign [list $t2 $t1] t1 t2 }
return [list $t1 $t2]
}
##+##########################################################################
#
# FindAngle3 -- returns the angle between three points
#
proc FindAngle3 {p1 p2 p3} {
lassign [VSub $p1 $p2] x1 y1
lassign [VSub $p3 $p2] x2 y2
set m1 [expr {sqrt($x1*$x1 + $y1*$y1)}]
set m2 [expr {sqrt($x2*$x2 + $y2*$y2)}]
set dot [expr {$x1 * $x2 + $y1 * $y2}]
set theta [expr {acos($dot / $m1 / $m2)}]
return $theta
}
##+##########################################################################
#
# RotateCC -- rotates vector v by beta radians counter-clockwise
#
proc RotateCC {v beta} {
lassign $v x y
set xx [expr {$x * cos(-$beta) - $y * sin(-$beta)}]
set yy [expr {$x * sin(-$beta) + $y * cos(-$beta)}]
return [list $xx $yy]
}
##+##########################################################################
#
# Cross -- returns the cross product -- easy w/ z=0
#
proc Cross {v1 v2} {
lassign $v1 x1 y1
lassign $v2 x2 y2
return [expr {($x1*$y2) - ($y1*$x2)}]
}
proc About {} {
set msg "Morley's Miracle\nby Keith Vetter, Feb 2003\n\n"
append msg "A whizzlet for visualizing Morley's Miracle. Drag any\n"
append msg "vertex and see Morley's Miracle in action.\n\n"
append msg "About a century ago, Frank Morley proved a curious\n"
append msg "theorem about triangles which has become known in\n"
append msg "mathematical folklore as Morley's Miracle.\n\n"
append msg "The theorem states that:\n"
append msg " The three points of intersection of the adjacent \n"
append msg " trisectors of the angles of any triangle form an \n"
append msg " equilateral triangle.\n\n"
append msg "See http://www.cut-the-knot.com/triangle/Morley/Morley.shtml\n"
append msg "for more details."
tk_messageBox -title "About Morley's Miracle" -message $msg
}
################################################################
DoDisplay
DrawLinesuniquename 2013jul29 This code should have some images to indicate what the script creates: