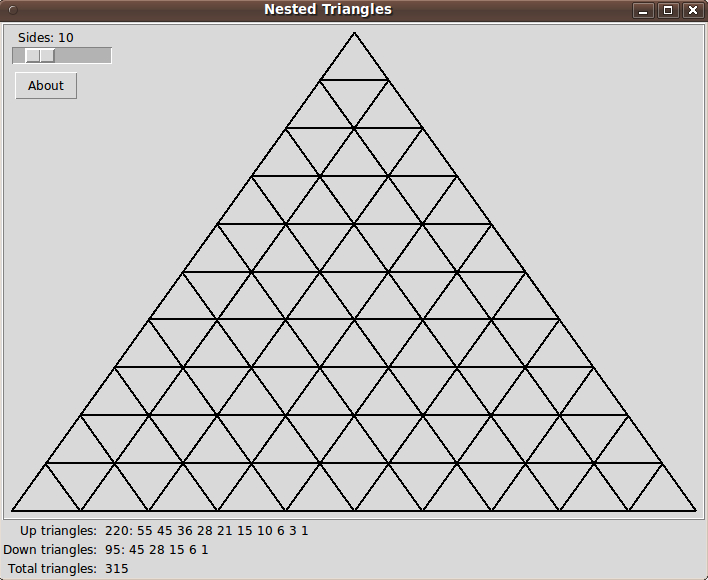
a triangle puzzle
Keith Vetter 2003-01-26
Start with an equilateral triangle then draw lines connecting the midpoints of each side. Now how many triangles are there? Answer: 5 -- three small "up" triangles, one "down" triangle plus the outer, larger triangles. Repeat the subdivision on all the smaller triangles and now how many triangles are there?
Counting the number of triangles in this type of figure is an old puzzle. Finding a general formula is even trickier.
This little program is a visualization of this problem. I found it while cleaning up my hard drive and I thought I'd share it here.
This is sequence A002717 on the On-line Encyclopedia of Integer Sequences. It has the closed for form: floor(n * (n+2) * (2n + 1) / 8)
##+##########################################################################
#
# triags -- Draws nested triangles and displays the total number of
# triangles there are and also shows how many triangles of each size.
#
# Keith Vetter Jun 24, 1998 - initial revision
#
##+##########################################################################
#
# DoDisplay -- puts up our interface
#
proc DoDisplay {} {
global w h
canvas .c -width $w -height $h -bd 2 -relief ridge
frame .bottom
scale .s -orient h -from 1 -to 50 -command DrawTriangles -showvalue 0 \
-variable S(n) -highlightthickness 0
set ::S(n) 3
focus .s
label .lcntU -text "Up triangles: "
label .lcntD -text "Down triangles: "
label .lcntT -text "Total triangles: "
label .cntU -textvariable S(up)
label .cntD -textvariable S(down)
label .cntT -textvariable S(total)
catch {image create photo ::img::blank -width 1 -height 1}
button .about -image ::img::blank -highlightthickness 0 -command {
tk_messageBox -title "About" -message "by Keith Vetter\nJanuary, 2003"}
pack .c -side top -fill both -expand 1
place .s -in .c -x 10 -y 5 -anchor nw
pack .bottom -side bottom -fill x
grid .lcntU .cntU -in .bottom
grid .lcntD .cntD -in .bottom
grid .lcntT .cntT -in .bottom
grid configure .lcntU .lcntD .lcntT -sticky e
grid configure .cntU .cntD .cntT -sticky w
grid columnconfigure .bottom 1 -weight 1
place .about -in .c -relx 1 -rely 1 -anchor se
update
bind . <Configure> {triag $S(n)}
}
##+##########################################################################
#
# DrawTriangles -- called when the number of sides changes.
#
proc DrawTriangles {n} {
global S CNT
.s config -label "Sides: $n"
triag $n
set S(up) [CountUp $n]
set S(down) [CountDown $n]
set S(total) [expr {$CNT(up) + $CNT(down)}]
}
##+##########################################################################
#
# triag -- draws an N sided triangle
#
proc triag {n} {
global w h alt len
set w [winfo width .c]
set h [winfo height .c]
set alt [expr {($h - 20.0) / $n}] ;# Scale to fit window
set len [expr {($w - 20.0) / $n}]
.c delete all
set b [GetBottom $n] ;# Bottom coords
set l [GetLeft $n] ;# Left side coords
set r [GetRight $n] ;# Right side coords
foreach {x1 y1} $l {x2 y2} $r { ;# Parallel to bottom
.c create line $x1 $y1 $x2 $y2 -width 2
}
foreach {x1 y1} $b {x2 y2} $r { ;# Parallel to left side
.c create line $x1 $y1 $x2 $y2 -width 2
}
foreach {x1 y1} [reverse $b] {x2 y2} $l { ;# Parallel to right side
.c create line $x1 $y1 $x2 $y2 -width 2
}
}
##+##########################################################################
#
# GetXY -- returns x,y coordinates for this triangle
#
proc GetXY {row col} {
global w len alt
set y [expr {round(10 + $row * $alt)}]
set x [expr {round($w/2.0 + $len * ($col - $row / 2.0))}]
return [list $x $y]
}
##+##########################################################################
#
# GetBottom -- returns coordinates of all bottom side vertices
#
proc GetBottom {n} {
for {set c 0} {$c <= $n} {incr c} {
eval lappend result [GetXY $n $c]
}
return $result
}
##+##########################################################################
#
# GetLeft -- returns coordinates of all left side vertices
#
proc GetLeft {n} {
for {set r 0} {$r <= $n} {incr r} {
eval lappend result [GetXY $r 0]
}
return $result
}
##+##########################################################################
#
# GetRight -- returns coordinates of all right side vertices
#
proc GetRight {n} {
for {set r 0} {$r <= $n} {incr r} {
eval lappend result [GetXY $r $r]
}
return $result
}
##+##########################################################################
#
# reverse -- reverses a list (by pairs)
#
proc reverse {l} {
set r ""
foreach {x y} $l {
set r "$x $y $r"
}
return $r
}
##+##########################################################################
#
# CountUp -- counts how many upright triangles there are.
#
proc CountUp {n} {
global CNT
set CNT(up) 0 ;# Reset all values to zero
for {set i 1} {$i <= $n} {incr i} {
set CNT(up,$i) 0
}
for {set row 0} {$row < $n} {incr row} {
set size 1
set num [expr {$n - $row}] ;# How many size 1 triangles
while {$num > 0} {
incr CNT(up,$size) $num
incr CNT(up) $num
incr num -1 ;# One less triangle at size+1
incr size
}
}
set v "$CNT(up): "
for {set i 1} {$i <= $n && $CNT(up,$i) > 0} {incr i} {
append v "$CNT(up,$i) "
}
return $v
}
##+##########################################################################
#
# CountDown -- same as count but for upside down triangles
#
proc CountDown {n} {
global CNT
set CNT(down) 0 ;# Reset all values to zero
for {set i 1} {$i <= $n} {incr i} {
set CNT(down,$i) 0
}
for {set row 0} {$row < $n-1} {incr row} {
set size 1
set num [expr {$n - $row - 1}] ;# How many size 1 triangles
while {$num > 0} {
incr CNT(down,$size) $num
incr CNT(down) $num
incr num -2 ;# Two less triangles at size+1
incr size
}
}
set v "$CNT(down): "
for {set i 1} {$i <= $n && $CNT(down,$i) > 0} {incr i} {
append v "$CNT(down,$i) "
}
return $v
}
set w 276
set h 276
DoDisplay
update
wm geom . [wm geom .] ;# Keeps window from growing
.c config -width 0 -height 0 ;# Better resizing behavioruniquename 2013jul29
This code could use an image to show what it produces:
(Thanks to 'gnome-screenshot', 'mtpaint', and ImageMagick 'convert' on Linux for, respectively, capturing the image to a PNG file, cropping the image, and converting the PNG file to a JPEG file that was about 8 times smaller. Thanks to FOSS developers everywhere.)
To capture this image, I changed the initial default of 3 levels of triangles to 10.