New Prime Number Browser
New Ulam Spiral Browser is the installment in the Primal Screens series. A brief description of the browser is given here followed by the associated Tcl/Tk source files.
See Also
- Primal Screens
- The first browser in this seriews.
- Primal Screens— Part Two
- The second.
- Monster Prime Predicting Formula
- A simple formula that predicts a large number of prime numbers.
- Gerard Sookahet
- Has contributed numerous visualizations related to prime numbers.
- Ulam spiral
- The famous spiral visualization of prime numbers.
Description
The New Ulam Browser has two windows, a Control Window and a Canvas Window in which Ulam spirals are plotted. On startup the control window appears all by itself with the main control buttons at the top. To start, first choose between SQUARE or TRIANGULAR grids and then select one of the granularity buttons, Coarse Grid or Fine Grid . The corresponding Ulam spiral will then appear in the canvas window.
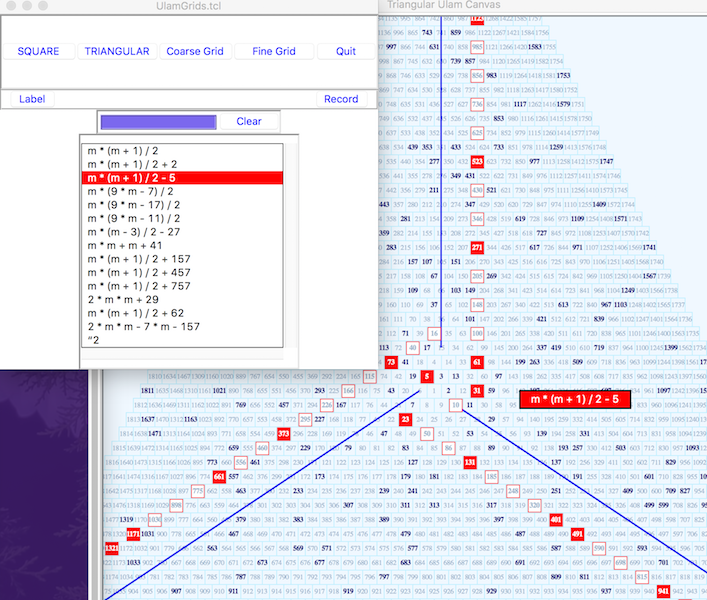
Figure 1 is a superposition of the two windows, with the control window in the foreground, top left, and part of the Coarse Triangular grid in the background. Normally, the two windows are separated, with the control panel off to the side of the plotting canvas. In Figure 1, the Coarse Triangular grid is tiled with small numbered squares. Prime Integers are in Bold and Navy Blue, non prime integers are in Gray. The three dark blue lines are the Principle Axes for this system. The listbox in the control panel shows the highlighted formula for the trajectory that is displayed. Primes on the trajectory are indicated by red squares with a bold white integer. Non Primes are white squares with red outlines and gray bold integers. The trajectory has three branches.
FIGURE 1
There are two buttons below the main buttons in the control panel. The first is for labeling a trajectory and the other for recording details of the trajectory. In Figure 1, the trajectory formula Label appears in red with white bold text.
Below these two buttons is a blue Entry Window and a Clear Button to the side. Below that is a listbox containing prime predicting formulae. Once the granularity has been selected, a mouse click on any formula in the listbox causes the trajectory for that formula to be overlaid on the Grid. In the Square Grid representation, a formula trajectory has two branches. In the Triangular representation, a trajectory has three.
For the Fine Resolution Grid, primes are designated simply as small blue plus signs. For a given trajectory in the Fine grid, primes are designated by small colored squares and non primes are small circles outlined in the same color. On either grid, an existing trajectory can be removed by clicking a second time on its previously selected formula in the listbox.
In figure 1, the formula m * ( m + 1) / 2 - 5 was selected from the listbox and portions of the three branches of it's trajectory appear on the canvas.
The blue formula entry window above the listbox is used to enter formulae for new trajectories. First click in the blue entry window to enter a new formula, then type in the formula. The formula must be of the form 2 * m * m - m - 13, followed by a return. The lower case letter m represents an integer which is incremented along the trajectory and is the only variable the program recognizes. The new formula will be appended at the bottom of the formula listbox and it's trajectory will be plotted. The clear button must be pressed before another formula can be entered. Spaces have been added in this example for clarity and are not necessary for the calculation. The code for handling formulae is very simple and does not have the ability to handle entries such as M² .
FIGURE 2
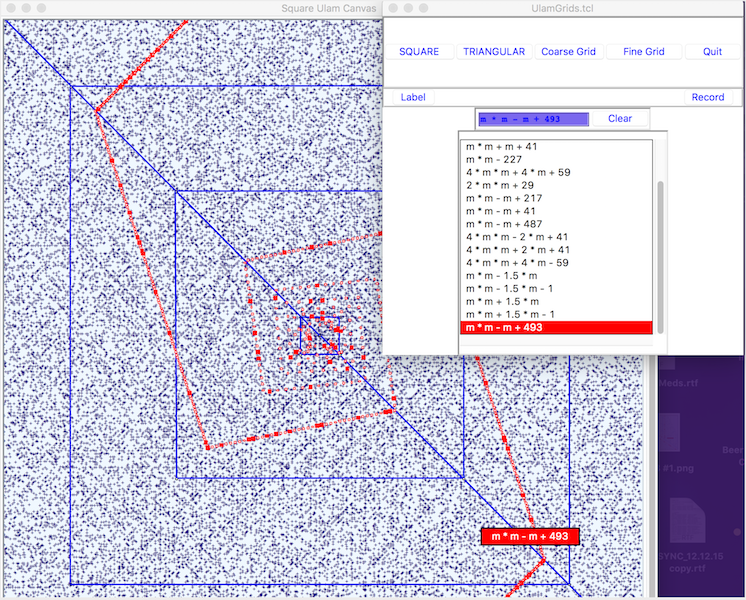
Figure 2 is another superposition of the control canvas and a portion of the plotting canvas, this time for the Fine Square Grid. In the plotting canvas, we now have a display of all primes that are less than 500K. The primes are indicated by the small Navy Blue plus signs. As mentioned in previous work, Primal Screens, the inner blue square represents the extent of the Coarse grid. The next outer square is the limit of all primes less than 100K and the last square confines all primes less than 300K.
The formula m * m - m + 493 was entered in the entry window and upon typing return, the formula was added at the bottom of the listbox. The formula’s trajectory and label were then displayed. Primes on the trajectory are indicated by small red squares, non primes are little circles outlined in red. The trajectory has two branches.
FIGURE 3
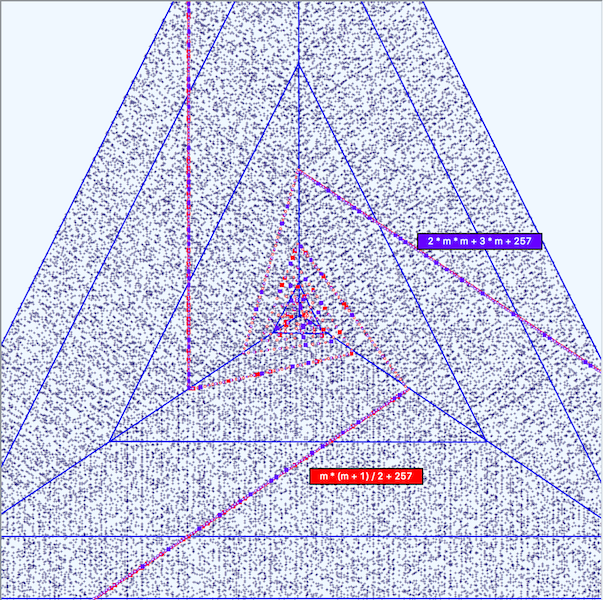
Finally, Figure 3 is thrown in just to show an interesting discovery. In the Fine Triangular Grid we see two distinctly different formulae which appear to have the same trajectory. The two formulae are: m * (m + 1) / 2 + 257 which calculates 89 Primes out of 988 predictions. for a Potency of 0.090 and 2 * m * m + 3 * m + 257 which calculates 87 Primes out of 493 predictions for a Potency of 0.176. The second formula strides through the field of primes twice as quickly as explained in Monster Prime Predicting Formula and has two fewer primes than the first formula.
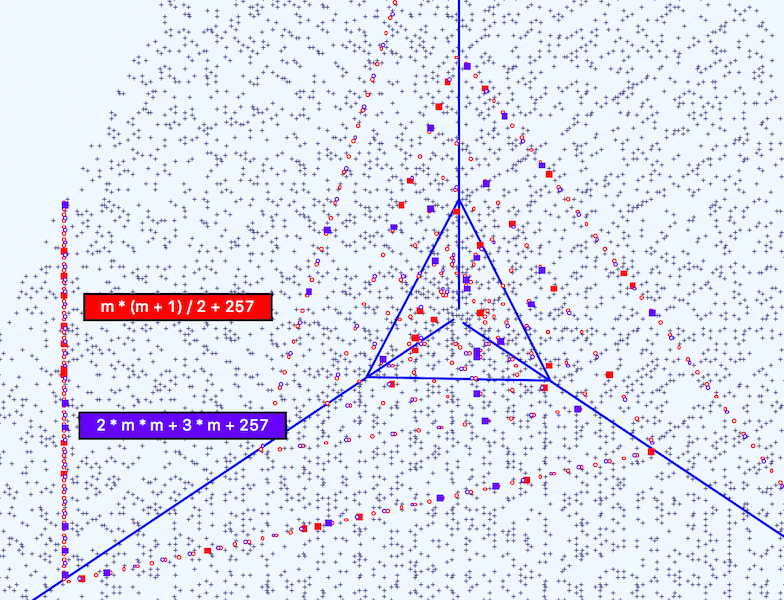
FIGURE 4
06.18.18 #2 copy
Upon further investigation, I discovered that my first assumption was incorrect. After printing out the primes and their corresponding values of m, two distinctly different sets of prime numbers showed up. Figure 4 above, shows that the two trajectories are very similar, but different. Here we see the two formulae plotted over a portion of the triangular set for all primes less than 100K. Notice the red and blue squares along the vertical branch near the left edge. At this resolution, they and the corresponding non primes are actually separated side by side. So there are really two distinct trajectories.
Need for a mathematician
The browser has raised several questions that perhaps a mathematician might try to answer.
Geometry based questions: In both systems, some trajectory branches have bends or breaks in direction. In formulae such as m * m - m + C, bends occur farther out as C increases. Often the bends occur as a branch crosses a Principle Axis and line segments between bends often are not aligned with the prime rich directions. What explains this behavior?
In both the Square and Triangular systems, prime rich directions are either parallel, anti-parallel or perpendicular to the Principle Axes. Why does this happen?
Why do two distinctly different formulae predict almost the same trajectories (see figs 3 and 4 above)?
Why are there prime rich directions in the first place and not just some random display? Why are some branches empty of primes? Perhaps these are satisfying questions for some mathematician.
Dedication
This is the last of the Primal Screen episodes. It has been difficult documenting all of this, mainly because Discovery has been much more fun than documenting. I’ve worked on the project on and off for some 15 years now, and as my son tells me about music projects— they are never finished, just abandoned. So, the Primal Screen project is now officially abandoned. I dedicate this work first of all to the memory of Stanislaw Ulam, who being blessed with a dull meeting and a quadrille tablet discovered what we now call Ulam Prime Spirals.
Next, I dedicate the following Tcl/Tk code to anyone who would venture further into this arena. I believe there is much yet to be discovered here and so this is for those hardy souls. I no longer have the time or energy to continue.
Future Directions
Here are some areas where someone might do further work:
Simple
—Working with the browser could be a nice project for advanced High School or beginning College students. They could learn something about Tcl/Tk coding and learn something about prime numbers by systematically varying formulae and posing their own questions. A better selection of colors could be made for plotting trajectories.
—Modify the code to make Clockwise Spirals. What would those trajectories look like for the same formulae? Instead of starting at integer 1, make the first starting square be something like 19. How would this affect the trajectories, potencies?
—What happens if one were to advance the set of primes to Primes LT 1,000,000? It would take some modification of the sizes of symbols, squares and screen size. Would Euler’s formula still be impressive for Primes Less than 1,000,000? Would a given formula still have bends further out?
More difficult
—Refactoring the code and adding new features. Trying other Grids— Hexagonal or Octagonal. What sort of formulae would be needed? Hint: See **Sloane’s On-Line Encyclopedia of Integer Sequences** oeis.org
Much More difficult
Create a magnifying glass for the Fine screen. It would be guided by cursor movements and would reveal a region around the cursor with enlarged readable numbers for the squares below. It would make discovering the closeness of trajectories such as found in Figure 4 much easier. I think this would be a difficult feature to implement.
The code itself
The current code is a melding of two previous separate browsers, one for Square geometry, the other for Triangular. Procs which had similar responsibilities in the two versions were mangled so as to eliminate overhead. The last of the known bugs has finally been smashed, but most likely there are still some that are not yet known. One caveat is that the code was developed on a Mac system and I don’t know how well it will translate to a Windoze machine.
The code will not run by itself without the companion file named PrimesList which the code sources upon startup. It must be in the same directory as the source code. In the early stages of this work, it was decided to create this list of prime numbers which could be searched, rather than having to calculate primes all the time. This allowed for a great speed advantage.
Two procs are included in the code which contain various formulae for the Square and Triangular grids. After selecting the granularity, the appropriate formulae will be entered in the Formula Listbox from one of these procs. If however, one of the files sq_Formula_File.tcl or tri_Formula_File.tcl is in the same directory as the browser, then formulae from the appropriate file will be placed in the listbox.
Stats on number of primes and speed of operation
I would have preferred to report on the speed at which the browser sources the list of Primes, followed by the speed of plotting a grid, but haven’t been able to figure out how to do that. All in all, it is FDQ (Fairly Darned Quick).
There are 41538 Primes Less Than 500,000. This means that for the Fine grid, a list of 41538 prime numbers is first sourced in, and then 500,000 small squares are calculated with 41538 plus marks at the appropriate positions. All of this happens rather rapidly on an iMac 4K Retina computer. For a typical formula, m * (m + 1) / 2 + 157, in the Triangular System, 988 predictions are made and 202 Primes are found, all rather quickly.
UlamGrids.tcl
#!/bin/sh
# \
exec wish "$0" ${1+"$@"}
# Latest Version: June 19, 2018
#
# This is file UlamGrids.tcl
#
# Procs appear in alphabetic order
#
# Keith W, Johnson
package require Tk
#
# First some global variables common to both Square & Triangular systems
set annotateIndex 0
set biggestPrime 0
set bkgndColor {}
set btmlft {}
set btmrt {}
set canvasWindow {}
set color {}
set commentString {}
set coordSystem {}
set Dbl_Button {}
set delta 20
set entryStrng {}
set fgndColor black
set fgndColorDx 0
set formCount 0
set formInput {}
set formulae {}
set formulaName {}
set formulasRead 0
set formList {}
set formNumberList {}
set foundPrime 0
set granularity {}
set haveGranularity 0
set ix 0
set iy 0
set labelButton 0
set labelId {}
set lastm 0
set lastPrime 0
set lastVertex {}
set lb {}
set nextOp "right"
set nucX 0
set nucY 0
set numIterations 5
set numPrimesCalcd 0
set out {}
set outLineColor lightblue1
set outString {}
set plusSize {}
set potency 0
set prevVertexNumber 1
set primeColor white
# Determine screen width.
set screenwd [winfo screenwidth .]
set srcFileName {}
set sqNum 1
set SQ_selected 0
set SQ_Formulas_Read 0
set startingIndex $sqNum
set tagName line
set top {}
set TR_selected 0
set TR_Formulas_Read 0
set twoDelta [expr {2*$delta}]
set vertexNumber 1
set vertexValues {}
set xRet 0
set yRet 0
set runningIndex [expr {$startingIndex - 1}]
# Thanks much to uniquename = Blaise Montandon for the following colors. I've
# rearranged them so there is a contrast between sequential selections. Colors
# are arranged into Background and Foreground colors.
set squareColors { {white black} \
{"#FF0000" white} {"#6600FF" white} {"#FFCC00" black} \
{"#0066FF" white} {"#FF6600" white} {"#00FF66" black} \
{"#FF00CC" white} {"#00BBFF" black} {"#1144FF" white} \
{"#CCDDBB" black} {"#BBFF00" black} {"#00BB00" black} \
{"#66FF55" black} {"#CC00FF" white} {"#FF0077" white}
}
#
set windowWidth [expr {int ( 0.5*$screenwd )}]
set winht $windowWidth
set x1 {}
set x2 {}
set y1 {}
set y2 {}
set xMin 10000
set xMex -10000
set yMin 10000
set yMax -10000
#
# PrimesList contains the list of Prime Numbers.
set src_Name "PrimesList"
if [file exists $src_Name] {
source PrimesList
} else {
puts "\n\n\n ----- Whoops! You need the list of Primes first. "
puts " This list should appear in the file PrimesList. \n"
puts " Use the file Primer.tcl to create this file. \n\n\n"
exit
}
set biggestPrime [lindex $primes end]
puts "\n\n --- biggestPrime is $biggestPrime, number of primes is [llength $primes] "
##------------------------------------------
## Proc array'reverse.
##
## A Proc to invert an array.
## Thanks to Example 8-4, "Practical Programming in Tcl and Tk"
## Brent B. Welch, 3rd Edn.
##
## Used in procs coarse doFormula and fine.
##-------------------------------------------
proc array'reverse { oldName newName } {
upvar 1 $oldName old $newName new
foreach {key value} [array get old] {set new($value) $key}
}
##------------------------------------------------------
## Proc coarse
##
## Create a Primal Screen using Coarse cells.
## Works for Sq and Tri systems
##
# If switching Geometries, the previous Ulam plot will
# not vanish until a new resolution is chosen.
#
# That is, if some plots were made in the Square Geometry
# and then you switch to Triangular, the Coarse
# or Fine buttons must then be selected before the Square
# Grid will disappear.
#
##------------------------------------------------------
proc coarse { } {
global btmlft btmrt canvasWindow coordSystem cX cY Dbl_Button delta formList
global formulasRead granularity haveGranularity labelButton labelId numIterations
global plusSize startingIndex top twoDelta V V2 vertexNumber windowWidth
set Dbl_Button {}
set delta 9
set formList {}
set formulasRead 0
set twoDelta [expr {2*$delta}]
set granularity "coarse"
set haveGranularity 1
set labelButton 0
set labelId {}
set numIterations 60
# set numIterations 30
set plusSize 9
set startingIndex 1
set vertexNumber 1
# Following are based on a delta of 9
set top 1770
set btmrt 1891
set btmlft 1830
set cX [expr {int ($windowWidth / 2)}]
set cY $cX
reset
puts " COARSE GRID \n"
createCanvas
drawSquares
$canvasWindow configure -scrollregion [$canvasWindow bbox all]
if {[string compare $coordSystem "tri"] == 0} {
array'reverse V V2
}
drawCoords
if {$formulasRead == 0} {
readFormulae
}
}
##----------------------------------------------------------------------------
## Proc composeFormula
##
## formInput is the formula that was entered in the entrybox in controlsSetup
## This new formula will be added to the end of the formula listbox.
##
##----------------------------------------------------------------------------
proc composeFormula { } {
global formCount formInput formulae lb
set formula {}
append formula "$formInput"
set formulaName "$formula"
set newForm [list $formulaName ]
lappend formulae $newForm
set lstboxString [format " %-s" $formulaName ]
$lb insert end $lstboxString
set idx [expr { $formCount -1}]
$lb see $formCount
formulaCalc $idx
incr formCount
}
##----------------------------------------------------------------
## Proc controlsSetup
##
## A proc to create the Controls canvas.
##
## Action Buttons and Formula Listbox are created in this canvas.
##
##----------------------------------------------------------------
proc controlsSetup { } {
global coordSystem entryStrng formInput formulasRead keepEntryStrng labelButton
global lastVertex lb nextOp out SQ_selected TR_selected vertexValues
# dumpFile accumulates comments when Record button is selected.
#
# set dumpFile "~/Unix_TCL/Projects/Prime_Ribs/Phase_One/Newest/MergeDir/LATEST/NEW_FormulaDumpFile"
set dumpFile "FormulaDumpFile"
set out [open $dumpFile "a"]
set entryStrng {}
set labelFont [font create -family courier -weight bold -size 12]
set xGeom1 1000
set yGeom1 50
wm geometry . +$xGeom1+$yGeom1
wm attributes . -topmost 1
focus .
# Determine screen width and height.
set screenwd [winfo screenwidth .]
# Create the controls canvas.
set fr1 [frame .fr1 -relief sunken -borderwidth 2 -height 30]
pack $fr1 -fill x -side top -in .
# Create the Top Buttons frame.
button $fr1.bSQ -text "SQUARE" -width 10 -bg white -fg blue \
-command {set coordSystem "sq"; set nextOp "right"; set $formulasRead 0; \
puts " SQUARE Coordinate System "; }
button $fr1.bTR -text "TRIANGULAR" -width 11 -bg white -fg blue \
-command {set coordSystem "tri"; set lastm 1; set lastVertex {}; \
set nextOp "tri_rt"; set prevVertexNumber 1; \
set vertexValues {}; set xRet 0; set yRet 0; set $formulasRead 0; \
puts " TRIANGULAR Coordinate System "; }
button $fr1.bCG -text "Coarse Grid" -width 10 -bg white -fg blue \
-command "coarse"
button $fr1.bFG -text "Fine Grid" -width 11 -bg white -fg blue \
-command "fine"
button $fr1.bQ -text Quit -width 8 -bg white -fg blue \
-command newExit
pack $fr1.bSQ $fr1.bTR $fr1.bCG $fr1.bFG -side left
pack $fr1.bQ -side right
set fr1b [frame .fr1b -relief groove -borderwidth 2 -height 30]
pack $fr1b -fill x -side top -in .
# Create the Label/Record Frame.
button $fr1b.label -text "Label" -width 6 -bg white -fg blue \
-command { set labelButton 1; drawAnnotationLabel }
button $fr1b.record -text "Record" -width 7 -bg white -fg blue \
-command "makeCommentWindow"
pack $fr1b.label -side left -padx 10
pack $fr1b.record -side right -padx 10
frame .f2 -relief sunken -borderwidth 2
frame .f2.title
pack .f2.title -side top
# Create the Formula EntryBox and Clear Frame.
#
# New formulae can be entered in this entry box. Once entered and followed
# by Return, the new formula will be added at the end of the formula listbox and the
# trajectory for this formula will be calculated and displayed.
#
# Formulae must be entered like following: m*m -38*m + 16
frame .f2.a
entry .f2.a.entryA -width 20 -relief ridge \
-font $labelFont -bg "medium slate blue" -fg blue
.f2.a.entryA insert end ""
button .f2.a.clr -text Clear -width 8 -bg red -fg blue \
-command {.f2.a.entryA delete 0 end; set formInput {}; set entryStrng {}}
pack .f2.a.entryA .f2.a.clr -side left
pack .f2.a -side left
pack .f2 -side top
# Create the Listbox Frame Next.
frame .f3 -relief sunken -borderwidth 2 -pady 10
text .f3.text -font "Courier 14" -wrap word \
-yscrollcommand {.f3.text_y set}
scrollbar .f3.text_y -relief groove -command {.f3.text yview}
set lb [listbox .f3.listbox -height 15 -width 28 \
-yscrollcommand [list .f3.lb_y set] -selectmode extended \
-xscrollcommand [list .f3.lb_x set] ]
scrollbar .f3.lb_y -orient vertical -command [list $lb yview]
scrollbar .f3.lb_x -orient horizontal -command [list $lb xview]
grid $lb -sticky nw -padx 1 -row 2 -column 1
grid .f3.lb_y -sticky nsw -padx 1 -row 2 -column 2
grid .f3.lb_x -sticky ew -padx 1 -row 3 -column 1
pack .f3 -side top
set fr4 [frame .fr4 -relief flat -borderwidth 2 -height 90]
pack $fr4 -fill x -side bottom -in .fr1
# proc formulaCalc will be invoked here, because a formula was selected from the listbox---
bind $lb <<ListboxSelect>> "formulaCalc -1"
# After completing formula entry and typing Return, add formula to bottom of listbox.
bind .f2.a.entryA <Return> {
set formInput $entryStrng
composeFormula
set entryStrng {}
break
}
# Text for Formula Entry handled here---
bind .f2.a.entryA <KeyPress> {
if {"%K" != "BackSpace"} {
append entryStrng %A
} else {
set strng [string range $entryStrng 0 end-1]
set entryStrng $strng
set formInput $strng
}
}
bind .fr1 <Enter> {
focus .fr1
}
.f3.text tag configure "matched" -background yellow
bind $fr1.bSQ <ButtonPress-1> {
set SQ_selected 1;
}
bind $fr1.bTR <ButtonPress-1> {
set TR_selected 1;
}
}
##------------------------------------------
## Proc createCanvas.
##
## Create the Ulam Spiral canvas. Sq or Tri.
##
##------------------------------------------
proc createCanvas { } {
global canvasWindow coordSystem windowWidth
set canvasWindow .w
set borderwidth 2
set hscroll $canvasWindow.hscroll
set vscroll $canvasWindow.vscroll
catch {destroy $canvasWindow}
toplevel $canvasWindow
if {[string compare $coordSystem "sq"] == 0} {
wm title $canvasWindow "Square Ulam Canvas"
} elseif {[string compare $coordSystem "tri"] == 0} {
wm title $canvasWindow "Triangular Ulam Canvas"
}
wm geometry $canvasWindow +100+100
focus $canvasWindow
canvas .w.c -relief sunken -borderwidth $borderwidth \
-width $windowWidth -height $windowWidth -bg "alice blue" \
-xscrollcommand "$hscroll set" \
-yscrollcommand "$vscroll set"
scrollbar $hscroll -orient horiz -command ".w.c xview"
scrollbar $vscroll -command ".w.c yview"
pack $hscroll -side bottom -fill x
pack $vscroll -side right -fill y
pack .w.c -side right -fill both -expand 1
set canvasWindow .w.c
update idletasks
}
##--------------------------------------------
## Proc doFormula
##
## Plot the trajectory of a chosen formula.
## Works for Sq and Tri systems.
##
##--------------------------------------------
proc doFormula { newFormName tagName } {
global biggestPrime bkgndColor coordSystem cX cY fgndColor formulaName
global foundPrime lastm lastPrime numPrimesCalcd out outString P
global potency startingIndex vertexNumber
# Invert the P array, so the X Y coords of Prime P can be obtained
# from the value of the Prime itself. P array is created in isPrime.
array'reverse P P2
set calcdPrimesList {}
set count 0
set formula "expr { int($newFormName)}"
set lastm 1
set mPrimesList {}
set num 0
set numPredicted 0
set numPrimesCalcd 0
set prevVertexNumber 1
# Create scripts for the two different coordSystems
if {[string compare $coordSystem "tri"] == 0} {
# Triangular coord system
set startingIndex 1
set vertexNumber 1
set script1 {
getTriCoords $num $tagName 1
}
} else {
# Square coord system.
set script1 {
set crds [getSqCoords $num 0]
getSqCoords $num 1
set x [lindex $crds 0]
set y [lindex $crds 1]
}
}
for {set m 2} {$m < $lastPrime} {incr m} {
set foundPrime 0
set num [eval $formula]
set ls [array get P2 $num]
set indx1 [expr {[string first " " $ls] -1}]
set indx2 [expr {[string first " " $ls] +1}]
set coord [string range $ls $indx2 end]
if { $num <= $lastPrime} {
incr numPredicted
incr count
} else { break }
if {![string match $coord ""]} {
# prime coords found
set foundPrime 1
incr numPrimesCalcd
set indx1 [expr {[string first "," $coord] -1}]
set indx2 [expr {[string first "," $coord] +1}]
set x [expr {[string range $coord 0 $indx1] + $cX}]
set y [expr {[string range $coord $indx2 end] + $cY}]
# Plot the Prime
plotSquare $num $x $y $fgndColor $bkgndColor $tagName 1
lappend calcdPrimesList "$num"
lappend mPrimesList "$m"
} else {
# non-prime coords found
# a formula may predict some negative values for num.
if {($num > 1.0) && ($num <= $lastPrime)} {
eval $script1
}
}
}
set numCoarse 0
set numPrimesCalcd 0
set calcdListLeng [llength $calcdPrimesList]
for {set i 0} {$i <= $calcdListLeng } {incr i} {
# last prime in coarse grid is 3593.
if { [lindex $calcdPrimesList $i] < 3593} {
incr numCoarse
}
if { [lindex $calcdPrimesList $i] < 500000} {
incr numPrimesCalcd
}
}
# After plotting all primes for this trajectory, do final stuff here.
incr numCoarse -1
incr numPrimesCalcd -1
set potency [format "%6.3f" [expr { $numPrimesCalcd / double($count) }] ]
puts "\n -- formula $formulaName calculates \
$numPrimesCalcd Primes out of \
$count predictions. \n Potency is $potency \n"
set firstPrime [lindex $calcdPrimesList 0]
set lastcalcdPrime [lindex $calcdPrimesList end]
set dt [clock format [clock seconds] ]
set outString "\n $coordSystem -- $dt --, \n $formulaName | $biggestPrime | \
$firstPrime | $lastcalcdPrime | $numCoarse | $numPrimesCalcd | $numPredicted | \
$potency, \n\n Calculated Primes: m,prime \n "
# Output values of m and corresponding Prime to dumpFile
for {set j 0} {$j <= $calcdListLeng} {incr j} {
append outString " [lindex $mPrimesList $j]," "[lindex $calcdPrimesList $j] \n "
}
}
##---------------------------------------------------------------------------
## proc drawAnnotationLabel
##
## A proc to place an annotation label at some position on the canvas.
## The label is the character string for the plotted formula.
#
## First, click the Lable button, then Double click the mouse at the point
## where the left edge of the label is to be drawn.
## Somewhat Klunky!
##
##---------------------------------------------------------------------------
proc drawAnnotationLabel { } {
global annotateIndex bkgndColor canvasWindow Dbl_Button formList formulaName
global fgndColor labelButton labelId
set labelId {}
set Dbl_Button 0
if { [llength $formList] >= 1} {
set annotateIndex [ lindex [lindex $formList end] 0 ]
} else {
set annotateIndex [ lindex [ lindex $formList 0] 0 ]
}
bind .w <Double-Button-1> {
# To handle inadvertant Double-Button-1
if { $Dbl_Button ==1} break
set labelId {}
set xLoc [ expr {[winfo pointerx $canvasWindow] - [winfo rootx $canvasWindow] } ]
set yLoc [ expr {[winfo pointery $canvasWindow] - [winfo rooty $canvasWindow] } ]
set path $canvasWindow.label$annotateIndex
set labelName [ lindex [ lindex $formList end] 1 ]
# Colors for label are reversed
set labelId [label $path -relief solid -bg $fgndColor -fg $bkgndColor \
-text "$labelName"]
place $labelId -x $xLoc -y $yLoc
set Dbl_Button 1
set labelButton 0
set labelId {}
update idletasks
}
}
##------------------------------------------------------------------------
## Proc drawBounds.
##
## In the Fine representation, draw a triangle that approximates the
## limits of the Triangular Format Coarse Screen.
## or
## Draw a square that approximates the limits of the Square Format Coarse
## Screen. plotLine is a proc used in the Square Format representation.
##
## In both FINE representations, draw bounds for Primes less than 100K
## and 300K, in the case that there are primes GT 300K.
##
##-------------------------------------------------------------------------
#
proc drawBounds { } {
global biggestPrime coordSystem tagName
set tagName coarse_bounds
if {[string compare $coordSystem "sq"] == 0} {
# Plot the boundary for the Coarse Square Format Screen.
plotLine 1766 1891 blue2
plotLine 1891 1850 blue2
plotLine 1850 1807 blue2
plotLine 1807 1766 blue2
if {$biggestPrime > 100000 } {
# Bounds for Primes LT 100K
plotLine 98911 99226 blue2
plotLine 99226 99541 blue2
plotLine 99541 99857 blue2
plotLine 99857 98911 blue2
# Bounds for Primes LT 300k
plotLine 298117 298663 blue2
plotLine 298663 299210 blue2
plotLine 299210 299757 blue2
plotLine 299757 298117 blue2
}
} elseif {[string compare $coordSystem "tri"] == 0} {
# Plot the boundary for the Coarse Triangular Format Screen.
# Get x-y coords for the following integers.
set top 1770
set left 1830
set right 1891
TridrawLine $top $left blue2
TridrawLine $left $right blue2
TridrawLine $right $top blue2
if {$biggestPrime > 100000 } {
# Bounds for Primes LT 100K
set top 98346
set right 97903
set left 97461
TridrawLine $top $left blue2
TridrawLine $left $right blue2
TridrawLine $right $top blue2
# Bounds for Primes LT 500K
set top 488566
set right 489555
set left 490545
TridrawLine $top $left blue2
TridrawLine $left $right blue2
TridrawLine $right $top blue2
# Bounds for Primes LT 300K
set top 298378
set right 299151
set left 299925
TridrawLine $top $left blue2
TridrawLine $left $right blue2
TridrawLine $right $top blue2
}
}
}
##--------------------------------------------------------------------
## Proc drawCoords.
##
## Draw Coordinate Axes through those cells which are the Squares of
## Odd or Even numbers in the Square Format screen.
## or
## Overlay three blue Coordinate Axes on the Triangular Format Screen.
## plotLine is a proc used in the Square Format representation.
## TridrawLine is used in the Triangular Format representation.
#
## These are the Principle Axes in each system.
##
##---------------------------------------------------------------------
proc drawCoords { } {
global biggestPrime btmlft btmrt coordSystem granularity tagName top
if {[string compare $coordSystem "sq"] == 0} {
# Square Coord System
# Plot a line through the Even and Odd squares.
set tagName odd_even
if {[string compare $granularity "fine"] == 0} {
if {$biggestPrime < 100000 } {
plotLine 4 99857 blue2
plotLine 1 99226 blue2
} elseif {$biggestPrime > 100000 } {
plotLine 4 499849 blue2
plotLine 1 498436 blue2
}
} elseif {[string compare $granularity "coarse"] == 0} {
plotLine 4 14400 blue2
plotLine 1 14161 blue2
}
} elseif {[string compare $coordSystem "tri"] == 0} {
# Triangular Coord System
# Draw Axis 1 TO TOP
TridrawLine 15 $top blue2
# Draw Axis 2 TO BTM RIGHT
TridrawLine 10 $btmrt blue2
# Draw Axis 3 TO BTM LEFT
TridrawLine 6 $btmlft blue2
}
}
##------------------------------------------------------------
## Proc drawSquares.
##
## Plot a square cell at the proper location for each integer.
## For Coarse Screen, label each cell with integer. Indicate
## Prime numbers with colored text.
##
## For the square that completes a triangle in the Triangular
## Format, store that integer in array V, which will have
## indices x and y.
##
## Thus:
## -- Vertex V(9,-18) contains the integer 3
## -- Vertex V(-18,0) contains the integer 6
## -- Vertex V(27,18) contains the integer 10
## -- Vertex V(9,-54) contains the integer 15
## -- Vertex V(-45,18) contains the integer 21
## -- Vertex V(54,36) contains the integer 28
## -- Vertex V(9,-90) contains the integer 36
## -- Vertex V(-72,36) contains the integer 45
## -- Vertex V(81,54) contains the integer 55
##
##------------------------------------------------------------
proc drawSquares { } {
global color coordSystem cX cY delta lastVertex nucX nucY numIterations
global runningIndex startingIndex V vertexValues xMin xMax yMin yMax out
# Place the initial square cell here.
square $cX $cY
set runningIndex [expr {$startingIndex + 1}]
set nucX $cX
set nucY $cY
if {[string compare $coordSystem "tri"] == 0} {
# Triangular system here.
# Use following puts statement to print out Vertex numbers as shown above.
# puts " For delta = $delta, \n"
array unset V
for {set i 1} {$i <= $numIterations} {incr i} {
Tri_iterate $i
set VertexNum [expr {$runningIndex - 1}]
lappend vertexValues $VertexNum
set Xindex [expr {$nucX -$cX}]
set Yindex [expr {$nucY -$cY}]
# vertex coordinates are xindex and yindex.
set V($Xindex,$Yindex) $VertexNum
# Use following puts statement to print out Vertex Numbers as shown above.
# puts " Vertex V($Xindex,$Yindex) contains the integer $VertexNum"
# puts $out [expr {$VertexNum + 1}]
set lastVertex $VertexNum
}
} else {
# Square System here
array unset P
set color white
# Wrap inverted "L" or "L" shaped patterns around the initial cell.
for {set i 2} {$i <= $numIterations} {incr i} {
Sq_iterate $i
}
}
set xMin [expr {$xMin - $delta}]
set yMin [expr {$yMin - $delta}]
set xMax [expr {$xMax + $delta}]
set yMax [expr {$yMax + $delta}]
}
##------------------------------------------------------
## Proc fine
##
## Create a Primal Screen using Fine cells.
## Works for both Square and Triangular Format systems.
#
# If switching Geometries, the previous Ulam plot will
# not vanish until a new resolution is chosen, Coarse or
# Fine.
#
# That is, if some plots were made in the Square System
# and then you switch to Triangular, the Coarse
# or Fine buttons must be selected before the Square
# Grid will disappear.
##
##------------------------------------------------------
proc fine { } {
global biggestPrime btmlft btmrt canvasWindow coordSystem cX cY Dbl_Button
global delta formulasRead granularity haveGranularity labelButton labelId
global numIterations numPrimes plusSize primes startingIndex tagName top
global twoDelta V V2 vertexNumber windowWidth
set Dbl_Button {}
set granularity "fine"
set haveGranularity 1
set labelButton 0
set labelId {}
set startingIndex 1
set vertexNumber 1
set formulasRead 0
# For primes less than 100,000
if {$biggestPrime > 400000} {
set delta .6
set plusSize 6
} elseif {$biggestPrime > 100000} {
set delta .7
set plusSize 7
} elseif {$biggestPrime > 30000} {
# set delta 1
set delta 1.3
set plusSize 9
} else {
# For primes less than 30,000
set delta 2
set plusSize 9
}
set twoDelta [expr {2*$delta}]
puts "\n This is fine, delta is $delta \n"
# Integers at axis extremes for various sized prime fields.
if {$biggestPrime < 100000 } {
set top 98346
set btmrt 97903
set btmlft 97461
} elseif {$biggestPrime < 300000 } {
set top 298378
set btmrt 299151
set btmlft 299925
} else {
set top 488566
set btmrt 489555
set btmlft 490545
}
set numIterations [expr {int (sqrt ($biggestPrime) )}]
if {[string compare $coordSystem "tri"] == 0} {
set numIterations [expr {int (1.4 * $numIterations)}]
}
set cX [expr {int ($windowWidth / 2)}]
set cY $cX
reset
puts " FINE GRID \n"
createCanvas
drawSquares
$canvasWindow configure -scrollregion [$canvasWindow bbox all]
if {[string compare $tagName "refLines"] == 0} {
} else {
$canvasWindow delete coarse_bounds
}
if {[string compare $coordSystem "tri"] == 0} {
array'reverse V V2
}
drawCoords
drawBounds
set tagName refLines
set numPrimes [llength $primes]
if {$formulasRead == 0} {
readFormulae
}
}
##--------------------------------------------------------------
## Proc formulaCalc.
##
## When a Prime Predicting formula is entered in the entry box,
## or selected from the formula listbox, this proc is invoked to
## calculate the formula's trajectory. If iCompose > 0, then the
## formula has been entered in the entrybox and does not come from
## the formula listbox.
##
##---------------------------------------------------------------
proc formulaCalc { iCompose } {
global annotateIndex bkgndColor canvasWindow fgndColor formList formNumberList
global formulae formulaName haveGranularity lb prevVertexNumber tagName
global startingIndex vertexNumber
set vertexNumber 1
set prevVertexNumber 1
# Whoops, Must first specify granularity.
if {$haveGranularity < 1} {
puts "\n\n\n ----- You must specify a granularity first."
puts " ----- Click on Coarse Grid or Fine Grid before selecting a formula. \n\n"
return
}
if {$iCompose > 0} {
set idx $iCompose
} else {
set idx [$lb curselection]
}
# formString is used to make tags for individual trajectories so they can be deleted
# sometime in the future.
set formString "Formula"
# formList contains 4 elements, the index of the formula in the listbox, followed by
# the formulaName and then the foreground color and the background color.
# The colors are not necessarily linked with the individual formulas,
# but appear on a first come basis and are determined by proc set_Colors.
set srchPtrn [get_formNumber $idx $formList]
# Following is to handle the case where a previously selected formula is now to be
# inactivated in the formula listbox and the trajectory removed from the canvas.
if {[lindex $srchPtrn 0] > -1} {
set annotateIndex $idx
set tagName [append formString $idx]
$canvasWindow delete $tagName
set this "$canvasWindow.label$annotateIndex"
destroy $this
set annotateIndex 0
$lb selection clear $idx
repaint_formEntries $idx
listBoxRemove formList $srchPtrn
set tagName {}
set formNumberList [lsearch -all -inline -not -exact $formNumberList $idx]
return
}
# Proceed with formula calculation
lappend formNumberList $idx
set_Colors
set realFormNumber $idx
set formulaString [lindex $formulae $realFormNumber]
set formulaName [lindex $formulaString 0]
set tagName [append formString $realFormNumber]
lappend formList [list $idx $formulaName $fgndColor $bkgndColor]
$lb selection clear $idx
$lb itemconfigure $idx -foreground $bkgndColor
$lb itemconfigure $idx -background $fgndColor
update idletasks
set newFormName [search_formInputString $formulaName]
doFormula $newFormName $tagName
}
##---------------------------------------------------------
## Proc getSqCoords -- For Square Geometry
##
## A proc to calculate the x y coordinates for the square
## containing the integer num. If doPlot == 1, plot a
## small square at that location. This proc plots Prime
## and nonPrime numbers. The x,y coords are returned.
##---------------------------------------------------------
proc getSqCoords {num doPlot} {
global bkgndColor cX cY fgndColor tagName twoDelta
set srt [expr {int (sqrt ($num) )}]
set diff [expr {$num - $srt * $srt}]
if {[expr {fmod ($srt,2)}] > 0.0} {
set xsq_location [expr { $cX + ($srt/2) * $twoDelta}]
set ysq_location [expr { $cY + ($srt/2) * $twoDelta}]
if { $diff == 0} {
set x $xsq_location
set y $ysq_location
} elseif { $diff <= [expr { $srt + 1 }] } {
set x [expr {$xsq_location + $twoDelta}]
set y [expr {$ysq_location - $twoDelta * ($diff -1)}]
} else {
set x [expr {$xsq_location - $twoDelta * ($diff - $srt - 2)}]
set y [expr {$ysq_location - $twoDelta * $srt }]
}
} else {
set xsq_location [expr { $cX - ($srt/2 - 1) * $twoDelta}]
set ysq_location [expr { $cY - ($srt/2) * $twoDelta}]
if { $diff == 0} {
set x $xsq_location
set y $ysq_location
} elseif { $diff <= [expr { $srt + 1 }] } {
set x [expr {$xsq_location - $twoDelta}]
set y [expr {$ysq_location + $twoDelta * ($diff -1)}]
} else {
set x [expr {$xsq_location + $twoDelta * ($diff - $srt - 2)}]
set y [expr {$ysq_location + $twoDelta * $srt }]
}
}
plotSquare $num $x $y $fgndColor $bkgndColor $tagName $doPlot
if { $doPlot == 1 } {
plotSquare $num $x $y $fgndColor $bkgndColor $tagName $doPlot
} elseif {$doPlot == 2} {
plotSquare $num $x $y $fgndColor $bkgndColor $tagName $doPlot
}
return [list $x $y]
}
##-----------------------------------------------------------------
## Proc getTriCoords -- For Triangular Geometry
##
## A proc to calculate the x y coordinates in the Tri System for
## the square containing the integer num. The scheme is based on
## the coordinates for the triangular vertices which are stored in
## array V. If doPlot == 1, also plot a small square or circle at
## that location. This proc handles prime and nonPrime numbers.
## The x,y coords for the square are returned.
# The V2 array is the inversion of the V array and looks like:
# -- The Vertex V2(3) is located at 9,-18
# -- The Vertex V2(6) is located at -18,0
# -- The Vertex V2(10) is located at 27,18
# -- The Vertex V2(15) is located at 9,-54
# -- The Vertex V2(21) is located at -45,18
# -- The Vertex V2(28) is located at 54,36
# -- The Vertex V2(36) is located at 9,-90
# -- The Vertex V2(45) is located at -72,36
# The series 3 6 10 15 21 28 36 etc. are generated by the
# Formula m * (m+1) / 2. Except for the integer 3,
# this is the fundamental set of NON primes in the Tri System
# and these constitute the Principal Axes in the Tri System.
#
# The V array is created in the proc drawSquares.
# The proc tries to locate the two vertices that bound num.
# It then finds the x and y coordinates of num based on the
# coordinates of a vertex.
##
##-------------------------------------------------------------
proc getTriCoords {num tagName doPlot} {
global bkgndColor delta fgndColor lastm lastPrime lastVertex
global prevVertexNumber twoDelta V2 vertexNumber xRet yRet
# vertexNumber keeps track of which Triangular Axis we are dealing with.
set vertexNumber $prevVertexNumber
for {set m $lastm} {$m < $lastPrime} {incr m} {
set vtxnum1 [expr {($m + 1) * ($m + 2) / 2}]
set strng1 [array get V2 $vtxnum1]
set indx1 [expr {[string first " " $strng1] -1}]
set value [string range $strng1 0 $indx1]
if { fmod($vertexNumber,4) == 0} {
set vertexNumber 1
set prevVertexNumber 1
}
# puts "\n --- vtxnum1 is $vtxnum1, lastVertex is $lastVertex --- \n"
if {$vtxnum1 > $lastVertex} { break }
if {$value >= $num} {
# Find value of first Vertex greater than num.
incr indx1
set key [expr {[string range $strng1 $indx1 end] }]
# proc getVertex calculates xRet and yRet.
getVertex $key
set Diff [expr {$value - $num}]
if {$vertexNumber == 1} {
set x [expr { $xRet + $Diff * $delta}]
set y [expr { $yRet + $Diff * $twoDelta}]
} elseif {$vertexNumber == 2} {
set x [expr { $xRet + $Diff * $delta}]
set y [expr { $yRet - $Diff * $twoDelta}]
} elseif {$vertexNumber == 3} {
set x [expr { $xRet - $Diff * $twoDelta}]
set y $yRet
}
if {$doPlot == 1} {
plotSquare $num $x $y $fgndColor $bkgndColor $tagName 1
} elseif {$doPlot == 2} {
plotSquare $num $x $y white red $tagName 2
}
set lastm $m
return [list $x $y]
}
incr vertexNumber
incr prevVertexNumber
}
}
##----------------------------------------------------------------
## Proc getVertex
##
## A proc to extract the x and y Vertex Coordinates from key.
## Called from getTriCoords.
## Key looks like: 9,-54 for the Coarse Triangular Grid.
## Depending on delta, the integer at this location is 28.
## See documentation in drawSquares.
##----------------------------------------------------------------
proc getVertex { key } {
global cX cY xRet yRet
set strng1 $key
set indx1 [expr {[string first " " $strng1] +1}]
set indx2 [expr {[string first "," $strng1] -1}]
set indx3 [expr {[string first "," $strng1] +1}]
set xRet [expr {[string range $strng1 0 $indx2] + $cX}]
set yRet [expr {[string range $strng1 $indx3 end] + $cY}]
}
##---------------------------------------------------
## Proc get_formNumber
##
## Extract the formula number from the formula list.
##
##---------------------------------------------------
proc get_formNumber { index this_formList } {
# For description of this_formList see proc formulaCalc.
# This proc will return the index, foreground and background colors of the chosen
# formula which will be deleted from the active formulae in the formula listbox.
foreach lst $this_formList {
if {[lindex $lst 0] == $index} {
return $lst
}
}
return -1
}
##----------------------------------------------
## Proc isPrime.
##
## Determine if runningIndex is a Prime Number.
## If so, add this Prime to array P.
# The P array looks like this for the Coarse Square Format system:
# -- The Prime Number 2 is located at 18,0
# -- The Prime Number 3 is located at 18,-18
# -- The Prime Number 5 is located at -18,-18
# -- The Prime Number 7 is located at -18,18
# -- The Prime Number 11 is located at 36,0
# -- The Prime Number 13 is located at 36,-36
# -- The Prime Number 17 is located at -36,-36
# -- The Prime Number 19 is located at -36,0
# -- The Prime Number 23 is located at 0,36
# -- The Prime Number 29 is located at 54,-18
# -- The Prime Number 31 is located at 54,-54
# -- The Prime Number 37 is located at -54,-54
# -- The Prime Number 41 is located at -54,18
#
# The P array looks like this for the Coarse Triangular Format system:
# -- The Prime Number 2 is located at 18,0
# -- The Prime Number 3 is located at 9,-18
# -- The Prime Number 5 iis located at -9,-18
# -- The Prime Number 7 is located at -27,18
# -- The Prime Number 11 is located at 45,18
# -- The Prime Number 13 is located at 27,-18
# -- The Prime Number 17 is located at -9,-54
# -- The Prime Number 19 is located at -27,-18
# -- The Prime Number 23 is located at -36,36
# -- The Prime Number 29 is located at 72,36
# -- The Prime Number 31 is located at 54,0
# -- The Prime Number 37 is located at 0,-108
# -- The Prime Number 41 is located at -36,-36
##
##----------------------------------------------
proc isPrime { X Y } {
global color cX cY foundPrime lastPrime P primeColor
global primeIndex primes runningIndex
set foundPrime 0
set color white
if {[lindex $primes $primeIndex] == $runningIndex} {
set color $primeColor
set foundPrime 1
set lastPrime $runningIndex
set Xindex [expr {$X -$cX}]
set Yindex [expr {$Y -$cY}]
# Array P's index will be the X and Y coords of the found Prime number.
set P($Xindex,$Yindex) $lastPrime
incr primeIndex
}
incr runningIndex
}
##-------------------------------------------------
## Proc listBoxRemove.
##
## Unselect a previously selected listbox formula.
##
##-------------------------------------------------
proc listBoxRemove { listVariable value } {
global formulaName labelButton labelId
upvar 1 $listVariable var
set indx [lsearch -exact $var $value]
set var [lreplace $var $indx $indx]
destroy $labelId
set labelButton 0
set formulaName {}
}
##-----------------------------------------------------------------
## Proc makeCommentWindow
##
## Puts up a small window in which you can write a comment.
## Write outString and comment to out
##
##-----------------------------------------------------------------
proc makeCommentWindow { } {
global commentString out outString
set commentWindow .cmnt
set borderwidth 2
catch {destroy $commentWindow}
toplevel $commentWindow
wm title $commentWindow "Comment Window"
wm geometry $commentWindow +400+300
focus $commentWindow
label $commentWindow.l -text "Type Comment Here: "
entry $commentWindow.e -width 50 -relief ridge \
-font "Courier 14" -bg "alice blue" -fg "blue"
$commentWindow.e insert end " "
pack $commentWindow.l $commentWindow.e -side left -fill both -expand 1
focus $commentWindow
bind $commentWindow.e <Return> {
set commentString [.cmnt.e get]
puts $out "$outString "
puts $out "$commentString \n"
update idletasks
destroy .cmnt
}
}
##-----------------------------------
## Proc newExit.
##
## Before exiting, close file 'out'.
##
##-----------------------------------
proc newExit { } {
global out
close $out
exit
}
##--------------------------------------------------------------------
## Proc plotLine.
##
## Plot a line connecting the two integers, start and end with color.
##--------------------------------------------------------------------
proc plotLine {start end color} {
global canvasWindow tagName
set coords {}
set crds [getSqCoords $start 0]
set x1 [lindex $crds 0]
set y1 [lindex $crds 1]
set crds [getSqCoords $end 0]
set x2 [lindex $crds 0]
set y2 [lindex $crds 1]
lappend coords [list $x1 $y1 $x2 $y2]
eval {$canvasWindow create line} $coords \
{-tag $tagName -width 2 -fill $color}
}
##------------------------------------------------
## Proc plotSquare.
##
## Plot a square at x,y. For Coarse Granularity,
## emboss square with the integer num. For Fine
## plot a small plus if integer is prime, else plot
## a small circle if nonPrime.
##
##------------------------------------------------
proc plotSquare { num x y fgndColor bkgndColor tag doPlot } {
global canvasWindow foundPrime granularity plusSize
# Fine case.
if {[string compare $granularity "fine"] == 0} {
if {$foundPrime == 1} {
if {$doPlot ==1} {
sm_sq $x $y 2.4 $fgndColor $fgndColor $tag 1
}
} else {
sm_sq $x $y 1.4 white $fgndColor $tag 2
}
} else {
# Coarse case.
if {$foundPrime == 1} {
if {$doPlot ==1} {
sm_sq $x $y 8 $fgndColor $fgndColor $tag 1
$canvasWindow create text $x $y -text $num -fill $bkgndColor \
-font "Times $plusSize bold" -tag $tag
} elseif {$doPlot ==2} {
sm_sq $x $y 9 white $fgndColor $tag 2
$canvasWindow create text $x $y -text $num -fill $bkgndColor \
-font "Times $plusSize bold" -tag $tag
}
} else {
if {$doPlot ==1} {
sm_sq $x $y 8 white $fgndColor $tag 1
$canvasWindow create text $x $y -text $num -fill slategray3 \
-font "Times $plusSize bold" -tag $tag
} elseif {$doPlot ==2} {
sm_sq $x $y 8 white $fgndColor $tag 2
$canvasWindow create text $x $y -text $num -fill slategray3 \
-font "Times $plusSize bold" -tag $tag
}
}
}
}
##--------------------------------------------------------------
## Proc readFormulae.
##
## Read in the list of Formulae from the Formula files.
## There are separate files for Square and Triangular formats.
## For Sq system, the formula file is sq_Formula_File.tcl
## For Tri system, the formula file is tri_Formula_File.tcl
##
##---------------------------------------------------------------
proc readFormulae { } {
global coordSystem formCount formulae formulasRead
global lb srcFileName SQ_selected SQ_Formulas_Read
global TR_selected TR_Formulas_Read
set srcFileName {}
# Handle details for case where one Grid system was first selected and then later the
# other one is selected.
# Selecting Sq Grid after Tri Grid had been viewed.
if {[string compare $coordSystem "sq"] == 0} {
if {$TR_selected == 1} {
set TR_selected 0
set formulasRead 0
set formulae {}
$lb selection clear 0 end
}
# Selecting Tri Grid after Sq Grid had been viewed.
} elseif {[string compare $coordSystem "tri"] == 0} {
if {$SQ_selected == 1} {
set SQ_selected 0
set formulasRead 0
set formulae {}
$lb selection clear 0 end
}
}
if {[string compare $coordSystem "tri"] == 0} {
set srcFileName "tri_Formula_File.tcl"
if [file exists $srcFileName] {
source $srcFileName
} else {
if {$TR_Formulas_Read == 0} {
tri_GridFormulae
}
}
} else {
set srcFileName "sq_Formula_File.tcl"
if [file exists $srcFileName] {
source $srcFileName
} else {
if {$SQ_Formulas_Read == 0} {
sq_GridFormulae
}
}
}
set formCount 1
$lb delete 0 end
foreach form $formulae {
set formulaName [lindex $form 0]
set lstboxString [format " %-s" $formulaName ]
$lb insert end $lstboxString
incr formCount
}
$lb see 0
set formulasRead 1
}
##----------------------------------------------------------------
## Proc repaint_formEntries
##
## Remove the listbox background color of a formula that has been
## unselected from the formula listbox.
##
##----------------------------------------------------------------
proc repaint_formEntries { indx } {
global bkgndColor fgndColor lb
set fgndColor black
set bkgndColor white
$lb itemconfigure $indx -foreground $fgndColor
$lb itemconfigure $indx -background $bkgndColor
}
##----------------------------------------------------
## Proc reset
##
## Reset some global variables to initial conditions.
##
##----------------------------------------------------
proc reset { } {
global color coordSystem cX cY delta fgndColorDx formList
global formNumberList foundPrime lastm lastPrime lb nextOp nucX nucY
global prevVertexNumber primeColor primeIndex P runningIndex sqNum startingIndex
global tagName vertexNumber windowWidth xMin xMax yMin yMax
set color {}
set cX [expr {int ($windowWidth / 2)}]
set cY $cX
set fgndColorDx 0
set formList {}
set formNumberList {}
set foundPrime 0
set lastm 1
set lastPrime {}
if {[string compare $coordSystem "tri"] == 0} {
set nextOp "tri_rt"
set prevVertexNumber 1
set vertexNumber 1
} else {
set nextOp "right"
}
set nucX {}
set nucY {}
array unset P
set primeColor white
set primeIndex 0
set sqNum 1
set startingIndex $sqNum
set runningIndex [expr {$startingIndex - 1}]
set tagName line
set twoDelta [expr {2*$delta}]
set xMin 10000
set xMax -10000
set yMin 10000
set yMax -10000
foreach lst $formNumberList {
$lb itemconfigure $lst -background white
$lb itemconfigure $lst -foreground black
$lb selection clear $lst
}
set indx [$lb curselection]
if {$indx > 0} {
$lb selection clear $indx
}
}
##---------------------------------------------------------------
## Proc search_formInputString.
##
## This proc converts all m's in strng to $m's. $m is the
## variable that gets incremented in proc doFormula. m is for
## printing, $m is for calculating. Gloriously Klunky, no?
##
##---------------------------------------------------------------
proc search_formInputString { strng } {
set mcharreplace \$m
set modString ""
set inStringLeng [string length $strng]
set strngPosn 0
for {set i 0} {$i <= $inStringLeng } {incr i} {
set formChar [string range $strng $i $i]
if {$formChar == "m"} {
append modString "$mcharreplace"
} else {
append modString $formChar
}
}
return $modString
}
##-------------------------------------------------------------------
## Proc set_Colors.
##
## Choose foreground and background colors from array squareColors.
##
##-------------------------------------------------------------------
proc set_Colors { } {
global bkgndColor fgndColor fgndColorDx squareColors
if {$fgndColorDx < 16} {
incr fgndColorDx
} else {
set fgndColorDx 0
}
set fgndColor [lindex [lindex $squareColors $fgndColorDx] 0]
set bkgndColor [lindex [lindex $squareColors $fgndColorDx] 1]
}
##-----------------------------------------------------------------------
## Proc sm_sq.
##
## Draw a small square cell, centered on x and y with side length
## (2 * delt). Color square with color thisColor. Tag square
## with tagName. Depending on doPlot, plot either a square or a circle.
##
##-----------------------------------------------------------------------
proc sm_sq { x y delt thisColor outline tagName doPlot} {
global canvasWindow
# Calculate coords for small square.
set x1 [expr {$x - $delt}]
set y1 [expr {$y - $delt}]
set x2 [expr {$x + $delt}]
set y2 [expr {$y + $delt}]
if {$doPlot ==1} {
$canvasWindow create rectangle $x1 $y1 $x2 $y2 -fill $thisColor \
-width 1 -outline $outline -tag $tagName
} elseif {$doPlot ==2} {
$canvasWindow create oval $x1 $y1 $x2 $y2 -fill $thisColor \
-width 1 -outline $outline -tag $tagName
}
}
##------------------------------------------------------------------------------------
## Proc square.
##
## Draw a square cell for the integer sqNum, centered on x and y. If sqNum is Prime,
## enter the value of sqNum in Coarse grid, else use a '+' for Fine grid. Colorfill
## will be navy blue if integer is prime. For Coarse grid, nonprime integers will
## be written in slategray3. Cells will be 2 * $delta in width.
## Used in both the Sq and Tri systems.
##
##------------------------------------------------------------------------------------
proc square { x y } {
global canvasWindow delta foundPrime granularity sqNum xMin xMax yMin yMax
# isPrime will determine whether the integer at x,y is Prime, based on list of primes.
isPrime $x $y
# Determine min max extents of X and Y.
if {$xMin > $x} {
set xMin $x
} elseif {$xMax < $x} {
set xMax $x
}
if {$yMin > $y} {
set yMin $y
} elseif {$yMax < $y} {
set yMax $y
}
if {$foundPrime == 1} {
set fgnd "navy blue"
set weight bold
} else {
set fgnd "slategray3"
set weight normal
}
# Calculate coords for Square.
set x1 [expr {$x - $delta}]
set y1 [expr {$y - $delta}]
set x2 [expr {$x + $delta}]
set y2 [expr {$y + $delta}]
set outline lightblue1
# Create square here.
if {[string compare $granularity "fine"] == 0} {
} elseif {[string compare $granularity "coarse"] == 0} {
$canvasWindow create rectangle $x1 $y1 $x2 $y2 \
-outline $outline -width 1
}
# For coarse granularity, insert sqNum as text.
if {[string compare $granularity "coarse"] == 0} {
$canvasWindow create text $x $y -text $sqNum -fill $fgnd \
-font "Times 9 $weight"
} elseif {[string compare $granularity "fine"] == 0} {
if {$foundPrime == 1} {
$canvasWindow create text $x $y -text "+" -font "Times 7" \
-fill "navy blue"
}
}
incr sqNum
}
##-------------------------------------------------
## Proc sq_GridFormulae
##
## A proc that contains some default formulae for
## plotting Prime Predicting Trajectories in the
## Square system. These will appear in the
## Formula listbox unless the file
## sq_Formula_File.tcl exists. Formulae will be
## pulled from that file.
##-------------------------------------------------
proc sq_GridFormulae { } {
global formulae SQ_Formulas_Read
# 0 Principle Axes for Square System.
lappend formulae {"m * m" }
# 1 Only one branch with Primes.
lappend formulae {"m * m - 2" }
# 2 Only one branch with Primes.
lappend formulae {"m * m + 7" }
# 3 lagrange’s Formula.
lappend formulae {"m * m + m + 17" }
# 4 Variation on Euler.
lappend formulae {"m * m + m + 41" }
# 5 Only one branch with Primes.
lappend formulae {"m * m - 227" }
# 6 Collapsed to Lower right.
lappend formulae {"4 * m * m + 4 * m + 59" }
# 7 Spiral.
lappend formulae {"2 * m * m + 29" }
# 8 Euler like, three bends
lappend formulae {"m * m - m + 217" }
# 9 Euler’s Formula, no bends.
lappend formulae {"m * m - m + 41" }
# 10 Euler like, three bends, but further out.
lappend formulae {"m * m - m + 487" }
# 11 Collapsed to Upper right.
lappend formulae {"4 * m * m - 2 * m + 41" }
# 12 Collapsed to Lower left.
lappend formulae {"4 * m * m + 2 * m + 41" }
# 13 Collapsed to Lower right.
lappend formulae {"4 * m * m + 4 * m - 59" }
# 14 Square Empty. Empty to the right
lappend formulae {"m * m - 1.5 * m" }
# 15 Square Empty. Empty to the right
lappend formulae {"m * m - 1.5 * m - 1" }
# 16 Square Empty. Empty Downward
lappend formulae {"m * m + 1.5 * m" }
# 17 Square Empty. Empty Downward
lappend formulae {"m * m + 1.5 * m - 1" }
set SQ_Formulas_Read 1
}
##-------------------------------------------------
## Proc Sq_iterate
##
## A proc to write out the integers in Ulam order,
## on a SQUARE grid. Draw (2*$M -1) squares in
## an upside down L or backward L shaped pattern.
## Squares are drawn in Counter-ClockWise Order.
## Proc square draws the square.
##-------------------------------------------------
proc Sq_iterate {M} {
global nextOp nucX nucY twoDelta sqNum
set num_Moves [expr {$M -1}]
set nextOp "right"
if {[expr {fmod ($M,2)}] > 0.0} {
set nextOp "left"
}
if {[string compare $nextOp "right"] == 0} {
set nucX [expr {$nucX + $twoDelta}]
square $nucX $nucY
for {set i 1} {$i <= $num_Moves} {incr i} {
set nucY [expr {$nucY - $twoDelta}]
square $nucX $nucY
}
set cntr [expr {$sqNum -1}]
for {set i 1} {$i <= $num_Moves} {incr i} {
set nucX [expr {$nucX - $twoDelta}]
square $nucX $nucY
}
} else {
set nucX [expr {$nucX - $twoDelta}]
square $nucX $nucY
for {set i 1} {$i <= $num_Moves} {incr i} {
set nucY [expr {$nucY + $twoDelta}]
square $nucX $nucY
}
set cntr [expr {$sqNum -1}]
for {set i 1} {$i <= $num_Moves} {incr i} {
set nucX [expr {$nucX + $twoDelta}]
square $nucX $nucY
}
}
}
##--------------------------------------------------------------------
## Proc TridrawLine { start end color}.
##
## Draw a line with color from the number start to the number end on
## the Triangular Format Screen.
##
##---------------------------------------------------------------------
proc TridrawLine {start end color} {
global canvasWindow lastm tagName
set coords {}
set lastm 1
set topCoords [getTriCoords $start $tagName 0]
set lastm 1
set bottomCoords [getTriCoords $end $tagName 0]
set x1 [lindex $topCoords 0]
set y1 [lindex $topCoords 1]
set x3 [lindex $bottomCoords 0]
set y3 [lindex $bottomCoords 1]
lappend coords [list $x1 $y1 $x3 $y3]
eval {$canvasWindow create line} $coords \
{-tag $tagName -width 2 -fill $color}
}
##-----------------------------------------------
## Proc tri_GridFormulae
##
## This proc contains some default formulae for
## plotting Prime Predicting Trajectories in the
## Triangular system. These will appear in the
## Formula listbox unless the file
# tri_Formula_File.tcl exists. Formulae will be
# pulled from that file.
##-----------------------------------------------
proc tri_GridFormulae { } {
global formulae TR_Formulas_Read
# 0 Principle Axes for Triangular System.
lappend formulae {"m * (m + 1) / 2" }
# 1 Only one branch with Primes.
lappend formulae {"m * (m + 1) / 2 + 2" }
# 1 Only one branch with Primes.
lappend formulae {"m * (m + 1) / 2 - 5" }
# 2 Triangular Empty, Collapsed. Empty to the right.
lappend formulae {"m * (9 * m - 7) / 2" }
# 3 Triangular Empty, Collapsed. Empty to the left.
lappend formulae {"m * (9 * m - 17) / 2" }
# 4 Triangular Empty, Collapsed. Diagonal to Bottom Right.
lappend formulae {"m * (9 * m - 11) / 2" }
# 5 Triangular Empty. Only one Prime.
lappend formulae {"m * (m - 3) / 2 - 27" }
# 6 Variation on Euler. Spiral in Triangular System.
lappend formulae {"m * m + m + 41" }
# 7 Bends as Branches cross Principle Axes.
lappend formulae {"m * (m + 1) / 2 + 157" }
# 8 Bends as Branches cross Principle Axes.
lappend formulae {"m * (m + 1) / 2 + 457" }
# 9 Bends further out as Branches cross Principle Axes.
lappend formulae {"m * (m + 1) / 2 + 757" }
# 10 Branches are antiparallel to Principle Axes.
lappend formulae {"2 * m * m + 29" }
# 11 Similar to Previous, but Branches are Parallel to Principle Axes.
lappend formulae {"m * (m + 1) / 2 + 62" }
# 12 Similar to Previous, Branches are Parallel to Principle Axes.
lappend formulae {"2 * m * m - 7 * m - 157" }
# 13 Totally Empty. Mirror image of Principle Axes.
lappend formulae {"2 * m * m + 2" }
set TR_Formulas_Read 1
}
##---------------------------------------------------------
## Proc Tri_iterate
##
## A proc to write out the integers in Ulam order,
## but on a TRIANGULAR grid. Squares are drawn in
## Counter-ClockWise order. Proc square draws the square.
##---------------------------------------------------------
proc Tri_iterate {M} {
global delta nextOp nucX nucY twoDelta
if {[string compare $nextOp "tri_rt"] == 0} {
set nucX [expr {$nucX + $twoDelta}]
set nucY $nucY
square $nucX $nucY
for {set j 1} {$j <= $M} {incr j} {
set nucX [expr {$nucX -$delta}]
set nucY [expr {$nucY - $twoDelta}]
square $nucX $nucY
}
set nextOp "tri_up"
return
}
if {[string compare $nextOp "tri_up"] == 0} {
set nucX [expr {$nucX -$delta}]
set nucY [expr {$nucY - $twoDelta}]
square $nucX $nucY
for {set j 1} {$j <= $M} {incr j} {
set nucX [expr {$nucX - $delta}]
set nucY [expr {$nucY + $twoDelta}]
square $nucX $nucY
}
set nextOp "tri_dn"
return
}
if {[string compare $nextOp "tri_dn"] == 0} {
set nucX [expr {$nucX - $delta}]
set nucY [expr {$nucY + $twoDelta}]
square $nucX $nucY
for {set j 1} {$j <= $M} {incr j} {
set nucX [expr {$nucX + $twoDelta}]
set nucY $nucY
square $nucX $nucY
}
set nextOp "tri_rt"
return
}
}
### Start up everything here.
controlsSetup
########################## End of UlamGrids.tcl File #####################Primer.tcl
#
############### File Primer.tcl to roll your own list of Primes ###########
#
#
## How to run it--
#
#-- ./Primer.tcl
#
# --- Compute all primes that are less than: 2000
#
# There are 303 primes less than 2000
#
# Done
#
#!/bin/sh
# \
exec wish "$0" ${1+"$@"}
#
# Version of May 4, 2017
#
#### Calculate the Primes ####
set primes {}
puts -nonewline "\n --- Compute all primes that are less than: "
flush stdout
set max [gets stdin]
if {$max < 2} {
set max 2
}
set primes [list 2]
for {set test 3} {$test <= $max} {incr test 2} {
set maxTest [expr {int(sqrt($test))}]
foreach prime $primes {
if {$prime > $maxTest} {
lappend primes $test
break
}
if {![expr {$test % $prime}]} {
break
}
}
}
#### Put Primes into PrimesList file ####
set strng "# The Prime Numbers less than $max \n# \nset primes { \n"
set strngLen 2
set f [open "PrimesList" w]
foreach n $primes {
if {$strngLen > 75} {
puts $f $strng
set strng {}
set nLen [string length "$n "]
set strngLen $nLen
append strng "$n "
} else {
set nLen [string length "$n "]
incr strngLen $nLen
append strng "$n "
}
}
append strng "\n}"
puts $f $strng
close $f
puts "\n There are [llength $primes] primes less than $max \n"
exit
#======================== Output from Primer.tcl ===========================
#
# The Prime Numbers less than 2000
#
set primes {
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101
103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197
199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311
313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431
433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557
563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661
673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937
941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049
1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163
1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283
1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423
1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511
1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619
1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747
1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877
1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999
}
# There are 303 primes less than 2000
#
########################### End of Primer.tcl File #####################
#——
sq_Formula_File.tcl
——
#
############### File sq_Formula_File.tcl Next #############
#
#
#
# Following two have same Potency of 0.585 for Primes LT 100K
lappend formulae {"m * m - 7 * m - 97"}
lappend formulae {"m * m + 7 * m - 97"}
# Following two have same Potency of 0.148 for Primes LT 100
lappend formulae {"m * m - 7 * m + 97"}
lappend formulae {"m * m + 7 * m + 97"}
# Variations on a Theme. What happens when linear term in Formula is varied.
lappend formulae {"m * m - m - 97"}
lappend formulae {"m * m - 2 * m - 97"}
lappend formulae {"m * m - 3 * m - 97"}
lappend formulae {"m * m - 4 * m - 97"}
lappend formulae {"m * m - 5 * m - 97"}
lappend formulae {"m * m - 6 * m - 97"}
lappend formulae {"m * m - 7 * m - 97"}
lappend formulae {"m * m - 8 * m - 97"}
# More variations
lappend formulae {"m * m - 7 * m - 313"}
lappend formulae {"m * m - 8 * m - 127"}
lappend formulae {"m * m - 8 * m - 277"}
# These are best viewed with the PLT 500K Data Set
lappend formulae {"m * m - 225"}
lappend formulae {"m * m - 235"}
lappend formulae {"m * m - 237"}
lappend formulae {"m * m - 239"}
lappend formulae {"m * m - 240"}
lappend formulae {"m * m - 241"}
lappend formulae {"m * m - 253"}
lappend formulae {"m * m - 257"}
lappend formulae {"m * m - 271"}
lappend formulae {"m * m - 283"}
lappend formulae {"m * m - 295"}
lappend formulae {"m * m - 371"}
lappend formulae {"m * m - 971"}
lappend formulae {"m * m - 1372"}
# Other interesting Formulae
lappend formulae {"4 * m * m+ 4 * m + 409"}
lappend formulae {"m * m+ m + 409"}
lappend formulae { "m * m - 7 * m - 97"}
lappend formulae {"m * m - 2 * m - 41" }
lappend formulae {"m * m - 3 * m - 41" }
lappend formulae {"m * m - 4 * m - 41" }
# Almost the same trajectories. Collapsed into one Branch.
lappend formulae {"4 * m * m + 4 * m + 59"}
lappend formulae {"4 * m * m - 4 * m + 59"}
# Almost the same trajectories. Collapsed into one Branch.
lappend formulae {"4 * m * m + 4 * m - 59"}
lappend formulae {"4 * m * m - 4 * m - 59"}
# More Collapsed trajectories that are into one Branch.
lappend formulae {"4 * m * m + 3 * m + 59"}
lappend formulae {"4 * m * m - 3 * m + 59"}
lappend formulae {"4 * m * m + 3 * m - 59"}
lappend formulae {"4 * m * m - 3 * m - 59"}
#
#
#
########################### End of sq_Formula_File.tcl File #####################
#
#——
tri_Formula_File.tcl
——
#
############### File tri_Formula_File.tcl Next #############
#
#
#
#
# Following have almost the same trajectory.
lappend formulae {"m * (m + 1) / 2 + 257" }
lappend formulae {"2 * m * m + 3 * m + 257"}
#
# Following has primes on lines parallel to all three branches.
lappend formulae {"m * (m + 1) / 2 + 4" }
# Following has primes on lines parallel to branches 1 and 2.
lappend formulae {"m * (m + 1) / 2 - 4" }
# Following has primes on lines parallel to all three branches.
lappend formulae {"m * (m + 1) / 2 - 5" }
# Following has primes on lines parallel to all three branches.
lappend formulae {"m * (m + 1) / 2 + 7" }
lappend formulae {"m * (m + 1) / 2 + 57" }
lappend formulae {"m * (m - 1) / 2 + 57" }
lappend formulae {"m * (2 * m + 1) / 2 + 57" }
# Variations on a Theme. Best used with PLT 500K Primes List
lappend formulae {"m * (m + 1) / 2 + 57" }
lappend formulae {"m * (m + 1) / 2 + 157" }
lappend formulae {"m * (m + 1) / 2 + 257" }
lappend formulae {"m * (m + 1) / 2 + 357" }
lappend formulae {"m * (m + 1) / 2 + 457" }
lappend formulae {"m * (m + 1) / 2 + 557" }
lappend formulae {"m * (m + 1) / 2 + 657" }
lappend formulae {"m * (m + 1) / 2 + 757" }
# Following can be viewed with PLT 100K Primes List
lappend formulae {"2 * m * m + 3 * m + 59"}
lappend formulae {"2 * m * m + 4 * m + 59"}
# Variations on a theme. Modifying the constant term.
lappend formulae {"m * (m + 1) / 2 + 2"}
lappend formulae {"m * (m + 1) / 2 + 12"}
lappend formulae {"m * (m + 1) / 2 + 22"}
lappend formulae {"m * (m + 1) / 2 + 32"}
lappend formulae {"m * (m + 1) / 2 + 42"}
lappend formulae {"m * (m + 1) / 2 + 52"}
lappend formulae {"m * (m + 1) / 2 + 62"}
lappend formulae {" m * (m + 1) / 2 + 72 "}
lappend formulae {" m * (m + 1) / 2 + 82 "}
lappend formulae {" m * (m + 1) / 2 + 92 "}
lappend formulae {" m * (m + 1) / 2 + 102 "}
lappend formulae {" m * (m + 1) / 2 + 112 "}
#
#
#
########################### End of tri_Formula_File.tcl File #####################
#