Measuring Brinell Hardness with Hough Transformation using VecTcl
JMeh 17 Aug 2017 - HoughTrans
The Brinell test presses a 10 mm diameter hardened steel ball with a force of 29.42 kN into the surface of the material to be tested. After that the diameter of the impress is measured and then flows into a formula for calculating Brinell hardness. For a better measurement, the image of the impress is optically magnified on a milk glass disc, the screen. Since the size of the screen and the magnification factor are known, one can easily calculate the real diameter of the imprint if the size of the circle has previously been determined.
Therefore, I have installed a high resolution camera (1600x1200) in front of the screen to get a photo of the impress. Now one can use an analysis of the photo to find these points that form the edge of the imprint. With these points, a Hough transform can now be performed to determine the radius of the circle. This is the method which is used here.
Since the data volume in a Hough space becomes very large, it is not possible to store the values with standard Tcl commands. Therefore, the VecTcl library was used here.
If you want to learn more about Brinell Hardness or Hough Transformation, have a look at
https://en.wikipedia.org/wiki/Brinell_scale
https://en.wikipedia.org/wiki/Hough_transform
Yes, the performance of the algorithm using VecTcl is far away from being usable, but it is also more of a case study. You can see it working in this screencast (animated GIF):
The sample image of the camera can be downloaded here:
http://sesam-gmbh.org/images/Downloads/Public/hbcam.png
For performance reasons, I use the same algorithm but written in C at the real test facility. Here is a table of execution times of several implementations:
| Language | CPU type | number of steps | elapsed time | specials |
|---|---|---|---|---|
| Tcl | 2,6 GHz Intel Core i7 | 24 | 22.67 sec | Tcl with VecTcl commands |
| C# | 2,6 GHz Intel Core i7 | 360 | 0.894 sec | Running with mono on my MAC |
| C | 2,6 GHz Intel Core i7 | 360 | 1.036 sec | Pure C - Single Processor |
| C | 2,6 GHz Intel Core i7 | 360 | 0.454 sec | Pure C - OpenMP with 8 threads |
| CUDA | GeForce GTX 260 | 360 | 0.074 sec | GPU-Processing with 512 threads |
auriocus Nice! Apparently, lots of time is spent to transfer the photo image into a VecTcl array. There is a secondary package vectcl::tk which does the conversion in C (numarray::fromPhoto). It is fast enough for interactive frame rates, see https://www.youtube.com/watch?v=88J0tVFE_ic
DEC: Is the Tcl time without the puts's?
JMeh: There are only 24 puts in total (inside the loop) - that doesn't matter
DEC Do all the other code examples use a GUI? Just trying to understand where the time is used in the Tcl/Tk version and can it be improved.
JMeh: No, this one here is the only one with a GUI, but that's not the reason. Look at the source, I think, it's well documented. You will see several neted loops. The outer one "while alpha < fullCircle { ..." loops over each angle, it is followed by a loop over the radius "for ri = 0:m { ..." to determine the brightness value of the edge of the imprint, followed by a double loop over the coordinates of the hough volume "for y = 0:C_HEIGHT-1 { for x = 0:C_WIDTH-1 { ..." to accumulate the brightness in the hough volume. The whole is followed by the last triple loop over the whole hough volume to get the maximum, but it's supported by the max-vectcl function, which will speed it up dramatically, because on the average only every seventh pass requires a further search.
Let us calculate the effort (assuming a radius of 353 pixel):
| Step | Calculation | Number of passes | Sum |
|---|---|---|---|
| 1 | Determine brightness | 25 * 353 | = 8825 |
| 2 | Accumulate hough space | 25 * 250 * 250 | = 1562500 |
| 3 | Search maximum | 250 * 250 / 7 | = 9000 |
As you can see, the number of calculations is immensely high.
And here is the application:
#
# Hough Transformation Example
#
package require Tk
package require vectcl
namespace import vectcl::vexpr
set C_RANGE 125 ;# the radius in the hough volume
set C_WIDTH [vexpr {2 * C_RANGE}] ;# width of hough volume
set C_HEIGHT [vexpr {2 * C_RANGE}] ;# height of hough volume
set R_MIN 100 ;# minimum of valid radius
set R_MAX 550 ;# maximum of valid radius
set R_WIDTH [vexpr {R_MAX - R_MIN}]
set DEG_STEP 15 ;# search for edges every n degrees
set hotspotX 739 ;# X coordinate in the white spot
set hotspotY 605 ;# Y coordinate in the white spot
set scrnCenterY 675 ;# Y coordinate of the center of the screen
set scrnLeft 0 ;# X coordinate of the left bound of the screen
set scrnRight 0 ;# X coordinate of the left bound of the screen
set scrnWidth 0 ;# width of screen bounds
set scrnBrMin 250 ;# minimum screen brightness = 25 % (per mill)
set threshold 100 ;# minimum brightness difference = 10 % (per mill)
###############################################################################
proc MarkCenter {xc yc} {
vexpr {
x1 = xc -25
x2 = xc +25
y1 = yc -25
y2 = yc +25
}
.c create line $x1 $yc $x2 $yc -width 1 -fill #ff00ff
.c create line $xc $y1 $xc $y2 -width 1 -fill #ff00ff
update
}
proc MarkScreenBounds {} {
global scrnCenterY scrnLeft scrnRight scrnWidth
puts "screen bounds: $scrnLeft..$scrnRight = $scrnWidth pixel"
vexpr {
y = scrnCenterY
y1 = y -50
y2 = y +50
x1 = scrnLeft -30
x2 = scrnLeft
x3 = scrnRight
x4 = scrnRight +30
}
.c create line $x1 $y $x2 $y -width 2 -fill cyan -arrow last
.c create line $x3 $y $x4 $y -width 2 -fill cyan -arrow first
.c create line $x2 $y1 $x2 $y2 -width 1 -fill cyan
.c create line $x3 $y1 $x3 $y2 -width 1 -fill cyan
}
proc MarkPoint {alpha r xp yp br} {
puts [format " alpha=%5.3f r=%3d P=(%4d,%4d) br=%d" $alpha $r $xp $yp $br]
vexpr {
x1 = xp - 7
x2 = xp + 7
y1 = yp - 7
y2 = yp + 7
}
.c create oval $x1 $y1 $x2 $y2 -outline #ff0000 -fill {} -width 2
update
}
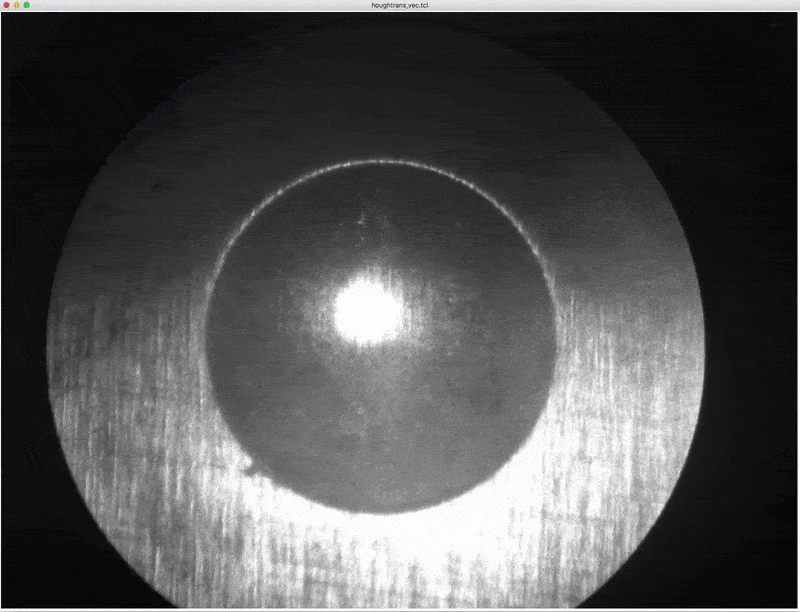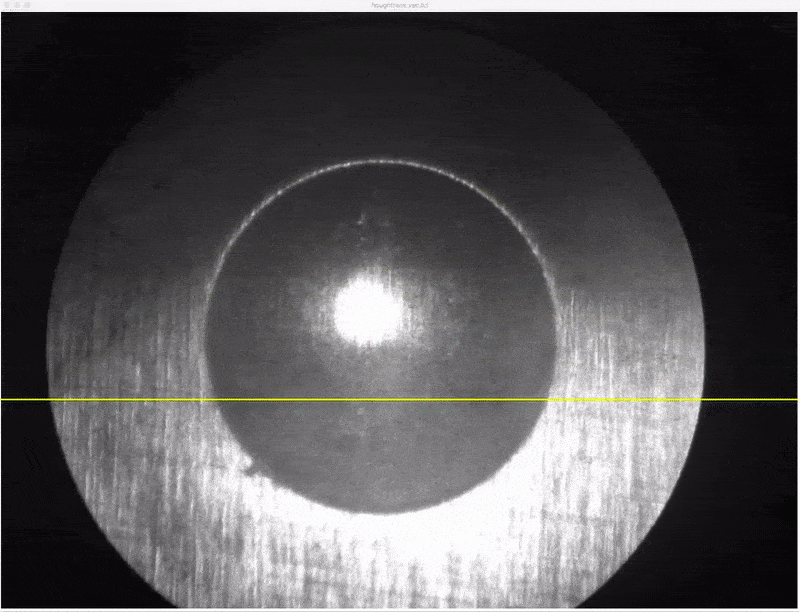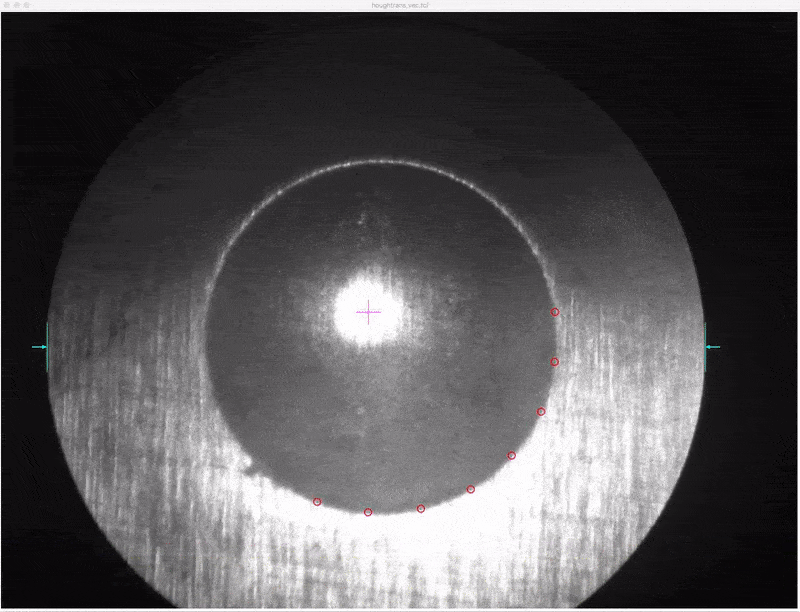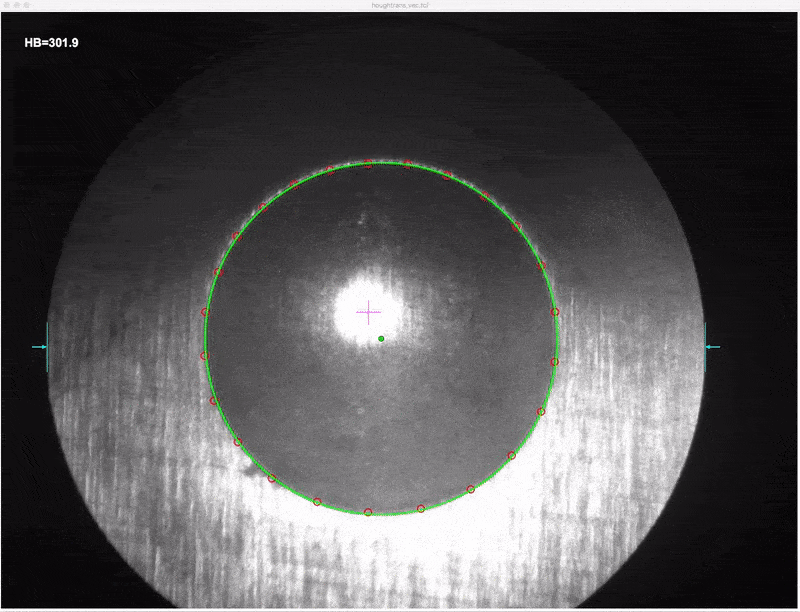
proc MarkImprint {h_max m_x m_y m_r} {
puts [format "h_max=%.0f @ P=(%u,%u) R=%u" $h_max $m_x $m_y $m_r]
vexpr {
x1 = m_x - m_r
x2 = m_x + m_r
y1 = m_y - m_r
y2 = m_y + m_r
}
.c create oval $x1 $y1 $x2 $y2 -outline #00ff00 -fill {} -width 3
vexpr {
x1 = m_x - 5
x2 = m_x + 5
y1 = m_y - 5
y2 = m_y + 5
}
.c create oval $x1 $y1 $x2 $y2 -fill #00ff00
update
}
proc ShowHB {hbval} {
.c create text 50 50 -anchor nw -font {Arial -24 bold} -fill white \
-text [format "HB=%.1f" $hbval]
}
###############################################################################
namespace import tcl::mathfunc::int
namespace import tcl::mathfunc::round
namespace import tcl::mathfunc::hypot
###############################################################################
proc CalcHB {rPixel} {
global scrnWidth
vexpr {
screenDiameter = 135.1 # diameter of the original screen in mm
enlargement = 20 # optical factor of the HB gauge
force = 29419.95 # pressure force in N
ballDiameter = 10 # ball diameter in mm
PI = 2 * asin(1.0)
# calculate the diameter of the imprint in mm
imprintDiameter = screenDiameter * 2 * rPixel / scrnWidth / enlargement
imprintDepth = 0.0 # the depth of the imprint
hbValue = 0.0 # the brinell hardness value
if imprintDiameter < ballDiameter {
imprintDepth = abs(ballDiameter - hypot(ballDiameter, imprintDiameter)) / 2
if imprintDepth > 0.0 {
hbValue = force / (9.80665 * PI * ballDiameter * imprintDepth)
}
}
}
puts [format "D=%.3f mm, d=%.3f mm, h=%.6f mm, HB=%.1f" \
$ballDiameter $imprintDiameter $imprintDepth $hbValue]
ShowHB $hbValue
return $hbValue
}
###############################################################################
proc houghtrans {} {
global C_WIDTH C_HEIGHT R_WIDTH C_RANGE R_MIN R_MAX DEG_STEP \
scrnCenterY scrnLeft scrnRight scrnWidth scrnBrMin \
hotspotX hotspotY threshold
set t_start [clock milliseconds]
puts "Houghtrans - Tcl edition"
puts "reading picture data ..."
image create photo hbcam -file hbcam.png
set w [image width hbcam]
set h [image height hbcam]
pack [canvas .c -width $w -height $h] -expand yes -fill both
.c create image 0 0 -image hbcam -anchor nw
update
# copy image into pixel (a vectcl 2D vector)
.c create line 0 0 $w 0 -width 3 -fill yellow -tags act_row
vexpr {pixel = constfill(0,h,w)} ;# create 2D pixel array
for {set y 0} {$y < $h} {incr y} { ;# for each row
if {$y % 5 == 0} {
.c coords act_row 0 $y $w $y ;# show where we are (sometimes)
update
}
for {set x 0} {$x < $w} {incr x} { ;# for each column
set red [lindex [hbcam get $x $y] 0]
vexpr {pixel[y,x] = red / 0.255} ;# set gray value (brightness) in per mill
}
}
.c delete act_row
MarkCenter $hotspotX $hotspotY
puts "searching edges ..."
vexpr {
# allocate 3D hough volume
houghdata = constfill(0,C_HEIGHT,C_WIDTH,R_WIDTH)
# search for left screen bound
searchLimit = w/4 # search up to 1/4 of the picture
scrnLeft = 0 # init left screen bound
x = 0 # start from left side
while x < searchLimit { # search from left to right
if pixel[scrnCenterY,x] > scrnBrMin { # search for more than x% brightness
scrnLeft = x # found left bound
x = searchLimit # finish loop
} else {
x += 1
}
}
# search for right screen bound
scrnRight = 0
searchLimit = 3*w/4 # search up to 3/4 of the picture
x = w-1 # start from right side
while x > searchLimit { # search from right to left
if pixel[scrnCenterY,x] > scrnBrMin { # search for more than x% brightness
scrnRight = x # found right bound
x = searchLimit # finish loop
} else {
x -= 1
}
}
scrnWidth = scrnRight - scrnLeft # this is the reference width
MarkScreenBounds() # show arrows for screen bounds
# search for edge of impression ...
fullCircle = 4 * asin(1.0) # 2 pi
delta = fullCircle / (360.0 / DEG_STEP) # angle step size
alpha = 0.0 # start at zero degrees
while alpha < fullCircle { # for each angle ...
br = 0 # init brightness
xp = 0 # init x coordinate of resulting point
yp = 0 # init y coordinate of resulting point
fx = cos(alpha) # vector x-scaling
fy = sin(alpha) # vector y-scaling
br_list = constfill(-1.0, 30) # make a vector for 30 brightness values
l = h / 2 # not more than half height of picture
m = l -1 # upper radius limit
r = 0 # resulting radius
for ri = 0:m {
x = hotspotX + round(fx * double(ri)) # calculate x coordinate
y = hotspotY + round(fy * double(ri)) # calculate y coordinate
if x > 0 && x < w && y > 0 && y < h { # is this point in my area?
db = 0 # reset brightness difference
br_list[29] = pixel[y,x] # save brightness of point in per mill
if br_list[0] != -1.0 { # if we have enough samples, calculate the jump
b1 = mean(br_list[0:24]) # inner brightness
b2 = mean(br_list[25:29]) # outer brightness
db = int(b2 - b1) # get brightness difference
}
br_list[0:28] = br_list[1:29] # shift the brightness buffer
if db > threshold { # minimum brightness reached
xp = x # set resulting x coordinate
yp = y # set resulting y coordinate
br = db # set resulting brightness
r = ri # set resulting radius
ri = m # finish, leave the loop
}
}
}
if r > 0 && r < l { # Found edge!
MarkPoint(alpha,r,xp,yp,br) # show where we are
for y = 0:C_HEIGHT-1 { # for each row in the hough volume ...
for x = 0:C_WIDTH-1 { # for each column in the hough volume ...
dx = xp - (hotspotX + x - C_RANGE) # x-distance from hotspot point
dy = (hotspotY + y - C_RANGE) - yp # y-distance from hotspot point
ri = int(hypot(dx, dy)) # calculate the radius of this point
if ri >= R_MIN && ri < R_MAX {
i = ri - R_MIN # radius index goes from R_MIN to R_MAX
houghdata[y,x,i] += br # add brightness value for this point
}
}
}
}
alpha += delta # next angle
}
# searching the hough volume for it's maximum value ...
h_max = -1
m_x = -1
m_y = -1
m_r = -1
for y = 0:C_HEIGHT-1 { # for each row in the hough volume ...
for x = 0:C_WIDTH-1 { # for each column in the hough volume ...
h_val = max(houghdata[y,x,:]) # search new maximum with vexpr max vector function
if h_val > h_max {
for r = 0:R_WIDTH-1 { # for each radius row in the hough volume ...
h_val = houghdata[y,x,r]
if h_val > h_max { # look for the greatest added brightness
h_max = h_val # my maximum value (until now)
m_x = hotspotX + x - C_RANGE # copy x coordinate
m_y = hotspotY + y - C_RANGE # copy y coordinate
m_r = r + R_MIN # copy radius
}
}
}
}
}
MarkImprint(h_max,m_x,m_y,m_r) # show the resulting circle and midpoint
CalcHB(m_r) # calc brinell hardness with the determined radius
}
set t_end [clock milliseconds]
puts [format "time=%.3f sec" [expr ($t_end - $t_start) / 1000.0]]
}
houghtrans