Ancient Egyptian Double False Position Algorithm, and example eTCL demo calculator, numerical analysis
Ancient Egyptian Double False Position Algorithm and eTCL demo example calculator, numerical analysis
gold 2018-12-12:
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks.
- Ancient Egyptian Double False Position Algorithm and eTCL demo example calculator, numerical analysis
- Pseudocode Section
- Appendix Code
- Comments
gold: Here is some eTCL starter code for ancient Egyptian double false position algorithm in calculator shell.
For purpose of historical discussion, the single and double false position methods will be lumped together, since the early authors and texts do not separate the terms or have some ambiguity. The rule of single false position is implied in the Ahmes Papyrus, 1650 BCE. On some Babylonian tablets like YBC4652 from 1500 BCE, there are corrected or rescaled false positions for the weight riddle problems. In some double position problems, negative numbers crop up. The Sunzi work in China cites the method of excess and deficit, circa 400 CE. The Chinese report some problems as double excess or double deficit, so there may have been differences the way some false position problems were set up, ref. Nine Chapters Mathematics (in extant copy circa 250 AD). Qusta ibn-Luqa of Baghdad (860 CE) discussed the double false position method in his work. In 1202 CE, Fibonacci wrote the Liber Abaci with some DFP problems. Clavius published some DFP discussion in the Epitome Arithmeticae Practicae in 1583 CE. In the USA, the textbook of Nicolas Pike (1788) presented the DFP rules fairly well, but later school textbooks with more on algebra dropped the issue. At least in Europe, the methods of double false position include early records and notation of negative numbers.
The Ancient Egyptians did not use algebra, but modern algebraic expressions can be developed for the Egyptian methods. The chosen false positions can be set as (3/5)*side_distance and (4/5)*side_distance, as used in the eTCL calculator. The false positions can be loaded in the product and two errors can be developed from initial goal minus product. Set error1 or e1 as (product-fx(f1)) and e2 as (product-fx(f2)). A modern algebraic expression for double false position is solution1 = (e2*f1-e1*f2)/(e2-e1), with the errors as e1&e2 and the false positions as f1&f2 . Using later notation for negative numbers (1600 CE) and multply nom and denom of expression by -1, variant solution2 = (e1*f2-e2*f1)/(e1-e2). Problems and variant solution2 may have been set up to avoid using or loading negative numbers, if e1>e2 or (e1*f2)>(e2*f1) in solution1.
Using modern Algebraic terminology, false position methods are used for one or more linear equations. For solving one linear equation with a single false position, find the number such that c1*x=c2 or fx(x)=c2 in other notation. Single false position would be solution3/f1 = fx/fx(b1), solution3 = (fx/fx(b1)) * f1 . For example 5*x=25 with fx=25 and 3 as the guess, solution3 = (fx/fx(b1)) * f1, solution3 = (25/15)* 3 , reduction (5/3)*3, solution3 = 5. For solution of two false positions with respective errors (e1&e2), the equations by definition are e1=(f1-fx) and e2 = (f2-fx) and as fractions 1= (f1-fx)/e1 and 1= (f2-fx)/e2. Substituting for 1, (f1-fx)/e1 = (f2-fx)/e2. Using rule of three, (f1-fx)/e1 = (f2-fx)/e2, (e1*(f2-fx))=(e2*(f1-fx)), e1*f2-e1*fx = e2*x1-fx*e2, fx*e2-e1*fx=e2*f1-e1*f2, fx*(e2-e1)=e2*f1-e1*f2, solution fx= (e2*f1-e1*f2)/(e2-e1).
For examples of double false position, 5*x=25 with fx=25 and 3&4 as the guesses, e1=(f1-fx), e1= 5*f1-25, e1=5*3-25,e1 = -10 and e2=(f2-fx), e2=5*4-25, e2 = -5. The solution fx= (e2*f1-e1*f2)/(e2-e1), fx=( -5*3)-(-10*4) / (-15--40),fx= 25/ 5, solution fx = 5. For another example 6*x=36 with fx=36 and 3&4 as the guesses, e1=(f1-fx), e1= 6*f1-36, e1=6*3-36,e1 = -18 and e2=(f2-fx), e2=6*4-36, e2 = -12. The solution fx= (e2*f1-e1*f2)/(e2-e1), fx=( -12*3)-(-18*4) / (-12--18),fx= 36/ 6, solution fx = 6. Using the algebraic equivalent expressions in the Babylonian weight riddle problems, an expression like x-x/7 or x*(1-(1/7)) are still simple multiples of the unknown x.
Looking at the Chinese and Arabic variants of the double false position expressions in modern algebra notation, there are ways to transform the formula expression (e2*f1+e1*f2)/(e2-e1) into weighted average of guesses like r1*( e2 /(e1+e2 ))+r2*( e1 /(e1+e2 ))= (e2*r1+e1*r2)/(e2+e1). Even a 3 way weighted average or 3 false position seems possible by adding another guess as r1*( e2 /(e1+e2 +e3 ))+r2*( e1 /(e1+e2 +e3 )) + r3*( e3 /(e1+e2 +e3 ))=(e2*r1+e1*r2 +e3*r3 )/(e2+e1+e3). For an algebraic analogy, multipart ratios are for distributing shares like 1:2:3...n in total sum(n) parts, where each brother in a sequence gets shares 1/(1+2+3...n), 2/(1+2+3...n),3/(1+2+3...n)... of the whole. The eTCL calculator works if negative errors are generated, but negative e1&e2 and negative error sums caused algorithm terminology and variants in early times. For study of the DFP algorithm in especially Chinese and Arabic variants, the eTCL logic can be changed to generate negative e1&e2.
The double false position formula depends on how the problem is worded. A word problem in the Arabic formula style can be solved by hand calculations and possibly suggestions for the eTCL calculator can be developed. A buyer with funds of 450 dinars wishes to purchase silk robes at 6 dinars each. How many robes of silk can be purchased with integer dinars? The guesses will be for the unstated conditions that silk robes are preferred and the vender expects baksheesh or gift of 36 dinars. The first guess of 50 silk robes is effectively 450-50*6=150 dinars low. The second guess of 80 silk robes is effectively 80*6-450=30 dinars high. The Arabic formula solution is (fp1*e2+ fp2*e2) / (e2+e1), substituting (50*30+ 80*150) / (30+150) =75 silk robes. The Arabic formula entries are all loaded as positive quantities or absolute value quantities. Checking 75*6 equals 450, the initial sum. The vendor returns 75 silk robes minus baksheesh(36/6) or 69 silk robes. In the initial calculations, the eTCL calculator returns 75.5 silk robes for entries of 6/3/450, since the calculator is loading the constant 3 and using decimals. For eTCL calculations with baksheesh (36), the eTCL calculator uses entries of 6/-36/450 and returns 69 silk robes. Continuing on to a modern algebra solution, 6*x + 36 = 450, x = (450-36)/6= 69 silk robes. Without baksheesh, 6*x = 450, x = 450/6, x = 75 silk robes. In the eTCL calculator, running absolute values in the DFP formula was considered, but thought too far from the original Egyptian algorithm.
A word problem called joint purchase in the Chinese formula style (210 CE) can be solved by hand calculations for double false position (DFP). A group of 9 gentlemen jointly buy a meal for 50 cash or coins. What was the contribution of each gentlemen in DFP? For false position of 7, the surplus is 7*9-50, or +13 coins. For false position of 4, the deficit is 50-4*9, or -14 coins. The Chinese formula solution is (fp1*e2+ fp2*e2) / (e2+e1), (7*14+4*13)/(14+13), or 5.555 cash. Loading 9/-5/50 into the eTCL calculator returns even 5 cash.. Loading 9/3/50 into the eTCL calculator returns 5.8 cash. An algebraic answer would be 9*x=50, x=50/9 or 5.555 cash.
An early mathematician apparently used the double false position (DFP) to attempt cube roots or other roots, although their extant documentation is ambiguous. Heron is reported to have used DFP to find the cube root of 100 as 4+9/14 (c. 100 CE). The DFP method can be treated as a type of interpolation for roots. The following are some examples of finding roots. Given that 2 is the cube root of 8 and that 3 is the cube root of 27, what is the cube root of 17, a prime number? The number 17 can not be factored and the cube root of 17 would not be a easy problem in Babylonian base60. Using 2 and 3 as the false positions, the error1 would be e1=17-8 or 9 and the error2 would be e2=27-17 or 10. The cube root (17) approximates the formula (fp1*e2+ fp2*e2) / (e2+e1), <expr (2*10.+3*9.)/(10.+9.) >, crt(17)~~ 2.4736842. The conventional eTCL root is <expr 17**(1./3.)> or 2.57128. The calculation error is <expr 100*(1-2.57128/2.4736842)> or root error 3.945 percent. Given that 4 is the cube root of 64 and that 5 is the cube root of 125, what is the cube root of 97, a prime number? Using 4 and 5 as the false positions, the error1 would be e1=97-64 or 33 and the error2 would be e2=125-97 or 28. The cube root (97) approximates the formula (fp1*e2+ fp2*e2) / (e2+e1), <expr (4.*28.+5.*33.)/(28.+33.) >, crt(97)~~ 4.5409836. The conventional root is <expr 97**(1./3.)> or 4.5947. The root error is <expr 100*(1-4.5947/4.5409836)> or root error 1.18 percent. The eTCL calculation selects the false positions by simple scaling, but the DFP logic and algorithm could be modified to select known roots, cubes, or other powers as boundaries of an interval containing the goal number.
The double false position method (DFP) can be treated as an iterated interpolation method for roots. Given that 18 is the cube root of 5832 and that 19 is the cube root of 6859, what is the cube root of 6247, a prime number? Using 5832 and 6859 as the false positions, the error1 would be e1=6247-5832 or 415 and the error2 would be e2=6859-6247 or 610. The cube root (6247) approximates the formula (fp1*e2+ fp2*e2) / (e2+e1), <expr (18.*610.+19.*415.)/(610.+415.) >, crt(6247)~~ 18.404878. The conventional root is <expr 6247**(1./3.)> or 18.4172097963212. The error is <expr 100*(1-18.4172/18.404878)> or 0.0669 percent. The target number 6247 is between 18.404878**3 and 19**3. Now use the calculated 18.404878 and 19 as false positions. The new root formula would be expr (18.404878*610.+19.*12.5402)/(610.+12.5402), root ~~ 18.416865. The error is <expr 100*(1-18.4172097/18.416865)> or root error ~~ 0.001867 percent. The target number 6247 is between 18.416865**3 and 19**3. Using the calculated 18.416865 and 19 as false positions, The new iterations on the root formula would be error1=6247 -18.416865**3 or e1~0.35085156, root ~ expr (18.416865*610.+19.*0.35085156)/(610.+0.35085156), root ~~ 18.4172002069. The error is <expr 100*(1-18.4172097/18.4172002069)> or root error ~~ 0.00005154 percent. The preceding indicates that finding roots with the ancient DFP formula and iteration is feasible, but not that the iteration DFP has more accurate calculations or faster convergence than current methods.
The Chinese used double false position (DFP) to interpolate the solution of a horse race problem in the Suanshu or Nine Chapters (commentary c. 260 CE). The Suanshu uses an indirect stage from direct questions (leap frog) or black boxes the error terms in modern terminology. Since this indirect stage of DFP problems is tricky, one can see why the some much later European works and even translations copied the easy stuff and dropped the indirect DFP methods in the Suanshu. Clearly, the available problems in the Suanshu show the versatility of the double false position method from joint purchases to horse races.
In the eTCL calculator, two false positions are supplied as guesses as false_position_1 <int <* $side_length >/ 4. 5. >>> and false_position_2 <int <* $side_length >/ 3. 5. >>> . Using the calculation methods, the two false positions produce numbers that fall short or long of the correct answer and the respective differences and errors are used to compute the final solution. A modern algebraic expression for double false position is (e2*f1-e1*f2)/(e2-e1), with the errors as e and the false positions as f. Some aspects of the double false position algorithm are similar to proportions and rule of three, as noted by many authors. The result is provided as </ $difference_cross_products $difference_error >. Note that brackets are set as <&> to avoid triggering wiki linkage.
The DFP logic switch is usually set to 1. Set DFP logic switch 1 for ++ false position errors, 2 for +-, 3 for --, or 4 for negative false position (override) entries. The DFP logic switches 2,3,4 check the calculator results for the Chinese and Arabian variant problems, which may generate negative e1&e2 and negative error sums. The eTCL seems to be working very well, getting a correct solution even with (override) negative entries.
Summary
Summary: The TCL calculator works with negative errors, but negative e1&e2 and negative error sums influenced algorithm terminology and variations in early times. The double false position formula varies depending on the problem wording. An example using the Arabic formula style involves a buyer with 450 dinars wishing to purchase silk robes at 6 dinars each, with calculations resulting in a solution of 75 silk robes.
| Mixed Signs and Logic Switches for DFP errors e1&e2 | tcl wiki format | ||
|---|---|---|---|
| quantity | value | comment, if any | |
| ++ : | double surplus | condition +e2>+e1, gets positive error | |
| +-: | mixed surplus deficit | condition +e2>(-e1), gets positive error | |
| -+: | mixed deficit surplus | condition (-e2)>+e1, gets negative error | |
| --: | double deficit | condition -e2>-e1, gets negative error | |
| ++ : | double surplus | set false_position_1 (int (* $side_length (/ 4. 5. ))) | |
| ++ : | double surplus | set false_position_1 (int (* $side_length (/ 3. 5. ))) | |
| +-: | mixed surplus deficit | set false_position_2 (int [* $side_length (/ 6. 4. ))) | |
| +-: | mixed surplus deficit | set false_position_2 (int [* $side_length (/ 3. 4. ))) | |
| --: | double deficit | set false_position_1 (int (* $side_length (/ 8. 4. ))) | |
| --: | double deficit | set false_position_2 (int (* $side_length (/ 6. 4. ))) | |
| note : | calculator works if negative errors generated | ||
| but neg e1&e2 and error sum caused terminology & varients in early times | |||
| eTCL logic can be changed for generating neg e1&e2 |
Pseudocode Section
# using pseudocode # possible problem instances, initialize algorithm_result = 1. set false1 [expr guess * 3/5] set false1 [expr guess * 4/5] calculate f(false1) and f(false2) error1 = product -f1 error2 = product -f2 [expr (e2*f1-e1*f2)/(e2-e1)] check algorithm f(solution) =? initial product check_sum = a+b+c+d+e = original real estate set answers and printout with resulting values pseudocode: need test cases > small,medium, giant pseudocode: need testcases within range of expected operation. pseudocode: are there any cases too small or large to be solved?
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
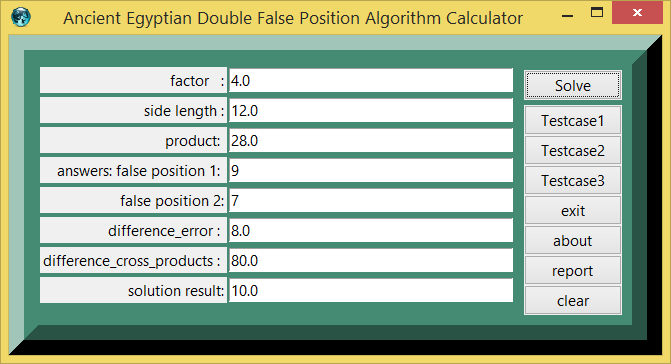
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 4.0 : | factor | |
| 12.0 : | side length | |
| 28.0 : | product | |
| 9 : | answers: false position 1 | |
| 7 : | false position 2 | |
| 8.0 : | difference_error | |
| 80.0 : | difference_cross_products | |
| 10.0 : | solution result |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 5.0 : | factor | |
| 10.0 : | side length | |
| 30.0 : | product | |
| 8 : | answers: false position 1 | |
| 6 : | false position 2 | |
| 10.0 : | difference_error | |
| 80.0 : | difference_cross_products | |
| 8.0 : | solution result |
Testcase 3
| 3: | testcase_number | |
| 6.0 : | factor | |
| 12.0 : | side length | |
| 36.0 : | product | |
| 9 : | answers: false position 1 | |
| 7 : | false position 2 | |
| 12.0 : | difference_error | |
| 96.0 : | difference_cross_products | |
| 8.0 : | solution result |
Testcase 4
| table 4, Arabic style problem | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 6.0 : | factor, price of silk robes | |
| -36.0 : | baksheesh as side length | |
| 450.0 : | product as dinars | |
| 1.0 : | optional: DFP logic switch (1,2,3,or 4,usually 1) | |
| -28 : | answers: false position 1 | |
| -21 : | false position 2 | |
| 1 : | logic_neg_errors 1 for ++, 2 for +-, 3 for --, 4 for neg. fps | |
| 582.0 : | error 1 | |
| 540.0 : | error 2 | |
| -42.0 : | difference_error | |
| -2898.0 : | difference_cross_products | |
| 69.0 : | solution result,69 robes for arabic style problem |
Testcase 5
| table 5, Chinese style problem | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 9.0 : | factor as gentlemen | |
| -5.0 : | side length , as a deficit of 5 coins | |
| 50.0 : | product as total coins for meal | |
| 1.0 : | optional: DFP logic switch (1,2,3,or 4,usually 1) | |
| -4 : | answers: false position 1 | |
| -3 : | false position 2 | |
| 1 : | logic_neg_errors 1 for ++, 2 for +-, 3 for --, 4 for neg. fps | |
| 81.0 : | error 1 | |
| 72.0 : | error 2 | |
| -9.0 : | difference_error | |
| -45.0 : | difference_cross_products | |
| 5.0 : | solution result, coins contribution lacking fraction, should be 5.55 coins |
Screenshots Section
figure 1.
References
- Chinese Horse Race Problems from Suanshu, DFP, and example eTCL demo calculator, numerical analysis
- Les neuf chapitres : le classique mathématique de la Chine
- ancienne et ses commentaires , in French and Chinese
- author(s) Karine Chemla, Guo Shuchun
- historia mathematica 1 (1974), 47-64
- The calculus of observations, a treatise on numerical mathematics
- reprinted 1954, rule of false position .....page 92
- by sir edmund whittaker,
- professor of mathematics in the university of Edinburgh
- and g. robinson, lecturer in mathematics in the university of edinburgh
- yang hui's commentary on the increase and decrease chapter of Suanshu
- by lam lay yong, university of singapore
- Suanshu English translation: Florian Cajori: Arithmetic in Nine Sections, 1893.
- Suanshu English translation: Lam Lay Yong: Jiu Zhang Suanshu,
- A Suanshu Overview, Archive for History of Exact Science, 1994
- Nine Chapters and Liu Hui's commentary,
- Nine Chapters on the Mathematical Art, Shen, Oxford 1999
- The Suanshu, Notes on Nine Chapters, Draft Notes. C. Cullen 2004
- Issues in the Origin and Development of Hisab al-Khata’ayn
- (Calculation by Double False Position), Randy K. Schwartz ,
- Eighth North African Meeting on the History of Arab Mathematics
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg,
- Chalmers University of Technology, Gothenburg, Sweden
- (major work on Babylonian inheritance problems)
- Muroi, Kazuo (1988). Inheritance problems of Babylonian mathematics.
- Historia Scientiarum , 34, 11-19
- Chabert, J. "Methods of False Position." Ch. 3 in A History of Algorithms: From the Pebble to the Microchip. , 1999.
- John Hannah , False position in Leonardo of Pisa's Liber Abbaci,Historia Mathematica Volume 34 issue 3 2007
- Eugene C. Boman,False Position, Double False Position and Cramer's Rule, College Mathematics Journal
- Howard Eves ,On the practicality of the rule of false position, Mathematics Teacher Volume 51
- Joy B. Easton, the rule of double false position, Mathematics Teacher Volume 60
- Vera Sanford, the rule of false position, Mathematics Teacher Volume 44 issue 5 1951
- Karine Chemla, Reflections on the World-wide History of the Rule of False Double Position, or: How a Loop Was Closed
- Thomas G. Edwards -- Using the Ancient Method of False Position to Find Solutions, Mathematics Teaching in the Middle School Volume 14 issue 4 2008
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
Appendix Code
appendix TCL programs and scripts
# TCL source code follows
# pretty print from autoindent and ased editor
# Ancient Egyptian Double False Position Algorithm V2
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL WIKI, 12Dec2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {factor :} }
lappend names {side length :}
lappend names {product: }
lappend names {optional, DFP logic switch (1,2,3,or 4,usually 1): }
lappend names {answers: false position 1: }
lappend names {false position 2:}
lappend names {difference_error : }
lappend names {difference_cross_products : }
lappend names {solution result:}
foreach i {1 2 3 4 5 6 7 8 9} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Ancient Egyptian Double False Position Algorithm V2
from TCL Club,
# gold on TCL WIKI, 12Dec2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg " Ancient Egyptian Double False Position Algorithm V2
from TCL ,
# self help listing
# problem, Ancient Egyptian Double False Position Algorithm V2
# 4 givens follows.
1) factor:
2) side length:
3) product:
4) optional, DFP logic switch (1,2,3,or 4,usually 1):
# Recommended procedure is push testcase
# and fill frame,
# change first three entries etc,
# push solve, and then push report.
# Report allows copy and paste
# from console to conventional texteditor.
# For testcases
# testcase number is internal to the
# calculator and will not be printed
# until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code
# is copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas
or math expressions grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 side9
global error_1 error_2 logic_neg_errors
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set side9 [* $side9 1. ]
set factor $side1
set side_length $side2
set product $side3
# initialize false positions
set false_position_1 9.
set false_position_2 10.
# reset false positions
# reset logic switch for neg e1&e2 and neg error sums
# set $logic_neg_errors 1 for ++, 2 for +-, 3 for --,
# set 4 for negative integer guesses
set logic_neg_errors [int $side4 ]
if { $logic_neg_errors == 1 } {set false_position_1 [int [* $side_length [/ 4. 5. ]]]}
if { $logic_neg_errors == 1 } {set false_position_2 [int [* $side_length [/ 3. 5. ]]]}
if { $logic_neg_errors == 2 } {set false_position_1 [int [* $side_length [/ 8. 5. ]]]}
if { $logic_neg_errors == 2 } {set false_position_2 [int [* $side_length [/ 3. 5. ]]]}
if { $logic_neg_errors == 3 } {set false_position_1 [int [* $side_length [/ 8. 4. ]]]}
if { $logic_neg_errors == 3 } {set false_position_2 [int [* $side_length [/ 6. 4. ]]]}
if { $logic_neg_errors == 4 } {set false_position_1 [int [* -1. $side_length [/ 8. 4. ]]]}
if { $logic_neg_errors == 4 } {set false_position_2 [int [* -1. $side_length [/ 6. 4. ]]]}
# end DFP logic switches
set false_result_1 [- [* $false_position_1 $factor ] $side_length]
set false_result_2 [- [* $false_position_2 $factor ] $side_length]
set error_1 [- $product $false_result_1]
set error_2 [- $product $false_result_2]
set difference_error [- $error_2 $error_1 ]
set difference_cross_products [- [* $false_position_1 $error_2 ] [* $false_position_2 $error_1 ] ]
set result [/ $difference_cross_products $difference_error ]
set side5 $false_position_1
set side6 $false_position_2
set side7 $difference_error
set side8 $difference_cross_products
set side9 $result
}
proc fillup {aa bb cc dd ee ff gg hh ii} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
.frame.entry9 insert 0 "$ii"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 9} {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8 side9
global error_1 error_2 logic_neg_errors
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|factor| |&"
puts "&| $side2 :|side length | |& "
puts "&| $side3 :|product | |& "
puts "&| $side4 :|optional: DFP logic switch (1,2,3,or 4,usually 1) | |&"
puts "&| $side5 :|answers: false position 1 | |&"
puts "&| $side6 :|false position 2 | |&"
puts "&| $logic_neg_errors :| logic_neg_errors 1 for ++, 2 for +-, 3 for --, 4 for neg. fps | |&"
puts "&| $error_1 :|error 1 | |&"
puts "&| $error_2 :|error 2 | |&"
puts "&| $side7 :|difference_error | |&"
puts "&| $side8 :|difference_cross_products | |&"
puts "&| $side9 :|solution result| |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 4.0 12. 28.0 1. 9.0 7.0 8.0 80.0 10.0}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 5.0 10.0 30.0 1. 8.0 6.0 10. 80.0 8.0}
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 6.0 12. 36.0 1. 9.0 7.0 12.0 96.0 8.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Ancient Egyptian Double False Position Algorithm V2 " Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
gold 2018-12-12: This page is copyrighted under the TCL/TK license terms, this license .
Comments
Please place any comments here with your WIKI moniker and date, Thanks, gold 12DEC2018
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |