Babylonian trailing edge algorithm and reverse sequence algorithm for reciprocals, eTCL demo example calculator, numerical analysis
Babylonian trailing edge algorithm and reverse sequence algorithm for reciprocals, eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Babylonian trailing edge algorithm and reverse sequence algorithm for reciprocals, eTCL demo example calculator, numerical analysis
- Pseudocode Section
- Appendix Code
- Console program under test.
- Console program for trailing edge reciprocal algorithm
- Console program for reverse_sequence_reciprocal algorithm
- Comments Section
gold Here is some eTCL starter code for Babylonian trailing edge algorithm and reverse sequence algorithm for reciprocals in calculator shell. Additional console programs below are used to check or improve subroutine.
gold Update 3/2/2024. This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core and Tcllib are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
Body
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written using a relative notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20. The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations and some units were left off the tablet. On the particular algorithms that use factoring, the relative value or uncertain magnitude makes a big difference because the factors of 20 and 1/20 are not the same. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the eTCL calculator can be run over a number of testcases to validate the algebraic equations.
The Babylonian trailing edge algorithm and reverse sequence algorithm from clay tablets was loaded into an eTCL calculator. This work is a follow on to the Babylonian irregular reciprocal calculator, but this wiki page places more emphasis on the number properties and the multiple algorithms for reciprocals in Babylonian use. In many cases, the Babylonians cited a reciprocal on a clay tablet, but the derivation or algorithm was not marked or known. The Babylonians did not use algebra notation, so the reader will have to bear some anachronisms in the eTCL pseudocode. The trailing edge algorithm is defined as the method used by scribes to successively factor a number to produce reciprocals. The reverse sequence algorithm is the inverse reciprocal or constructs a number from a known reciprocal, usually a reciprocal generated from previous use of trailing edge algorithm. There are features in the tablet display or factor selection that suggest that the reverse sequence algorithm is a didactic or expository work. Both the trailing edge algorithm and the reverse sequence algorithm have parallels to the Babylonian square root algorithm.
For the trailing edge concept, the number in specific base should have end digits on the trailing edge as factors of the base. The following discussion assumes that the numbers are written left to right, decreasing powers of selected base on right. The base 10 has factors 2*5 and numbers ending in 2/5 should be factorable by 2 or 5 respectively. For example, the number 12 is 2*3*3, factorable by 2. The number 125 is 5*5*5, factorable by 5. There are instances of end digits in base 10, where the trailing edge works occasionally, but not completely. The number 24 is 2*3*4 and factorable by 4, but 14 is 2*7, not factorable by 4. For the Babylonian base 60, the prime factors are 2/2/3/5. Meaning that the regular Bablylonian numbers that have end digits of 2/2/3/5 should be factorable by 2/2/3/5, at least. In base 60, 2.5 (decimal 125) has trailing edge of 5 and is factorable by 5. The numbers 7 and 17 are prime numbers and their trailing edges are not factorable by 2,2,3,5 in base 60. A prime number is prime in any base, so it may be inferred that the trailing edges of 7 and 17 would not be factorable in base 10. There are instances where the Bablylonian tablets are splitting off more than one power as the end factor. The eTCL code could either use the raw trailing edge concept or select from a list of known trailing edge factors in the limited tablet problems available. The eTCL code probably could use a fall back to a known list, if the split for trailing edge did not work. Not sure the method of trailing edge works for all n in any base, but the Babylonians are using this feature of base 60 in their algorithms to select factors.
For the base 10 system, several testcases of the trailing edge algorithm were developed with hand calculations. From tcl factoring, the prime factors of 525 are 3 5 5 7, in magnitude order. If the two edge digits are split off, the number 525 is indeed divisible by the factor 25. Using the easy eye calculator on this wiki, the reciprocal of 525 is 0.00190. Reduction of the target number to one and saving the treating factors as a product gives {(1./5.) *(1./5.)* (1./7.) * (1/3.) or reciprocal 0.0019 in the decimal system. These inverse prime numbers are associative, so the order of multiplication does not matter. Lets borrow one of the favorite Babylonian numbers, 60*60*60 or decimal 21600. The eTCl prime factoring gives <2 2 2 2 2 2 3 3 3 5 5 5>. The easy eye calculator gives the reciprocal or 1/21600 as 4.629629e-6. The reciprocal product would be <(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./3.)*(1./3.)*(1./3.)*(1./5.)*(1./5.)*(1./5.)> or 4.6296e-6. Quite a choker, but this is why the algorithms are loaded into the eTCL calculator. Lets look at the famous Babylonian mystic number 60*60*60*60 or decimal 12960000 years, 500 precessional cycles. The easy eye calculator gives the reciprocal 1/12960000, <expr 1./12960000.> or decimal 7.716049382716051e-8. The eTCL prime factors are <2 2 2 2 2 2 2 2 3 3 3 3 5 5 5 5> . The reciprocal product should be <expr (1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./3.)*(1./3.)*(1./3.)*(1./3.)*(1./5.)*(1./5.)*(1./5.)*(1./5.)>
For the base 10 system, several testcases of the reverse sequence algorithm were developed with hand calculations and based partly on the factors of the previous trailing edge algorithm calculations. The magnitudes for the factors in the reverse sequence algorithm have to be inferred, so these are really trial computations of consistent magnitude for factors on the reverse sequence math problems. For 10 in base10, the reciprocal is 1/10 or 0.10. The prime factors of decimal 10 are <2 5> . The non unique factors could be 1, 2*5 (10) from inspection of the available prime numbers and the observed sets of Babylonian factors. The reverse sequence algorithm is used to find the inverse reciprocal of 0.10. Multiply .10 by 2 for .2 and save the integer factor 2. Multiply .20 by 5 for 1 and save the integer factor 5. The number 0.10 is "reduced" or transformed into unity ( by selected factors of 10 ) and the integer factors saved for 2*5 = 10. Aside from the uncertain magnitude, the troubling part is that these reverse sequence factors were from the previous trailing edge calculations and the selection of these factors was not unique. For the testcases, the prime factors were selected but the Babylonians were selecting non unique factors, not only prime numbers.
Continuing to another testcase on reverse sequence algorithm, the reciprocal of 525 was 1/525 or decimal 0.0019 from the trailing edge reciprocal. The prime factors of decimal 525 are < 3 5 5 7 > . The non unique factors could be 1, 3*5 (15), 5**2(25), 5*7 (35), 3*5*5 (75), 5*5*7(175) from inspection of available prime numbers and the observed sets of Babylonian factors. Multiply 0.0019 by 3 for .0057 and save the integer factor 3. Multiplied 0.0057 by 5 for .0285 and save the integer 5. Multiply 0.0285 by 5 for 0.1425 and save the factor 5. Multiply 0.1425 by 7 for .9974 and save the integer 7. The number 0.0019 is transformed by selected factors of 525 into unity and the factors were saved for 3*5*5*7 = 525. The previous calculations for 525 used the prime number set, but like the Babylonians, non unique factors could be selected so long as the product of the selected factors equals 525. For a new set of calculations, multiply 0.0019 by 75 for 0.1425 and save the factor 75. Multiply 0.1425 by 7 for .9974 and save the integer 7. Two calculations were avoided in transforming 0.0019 to unity and the factors were saved for 75*7 = 525.
For a third test case on reverse sequence algorithm, the reciprocal of 48 was 1/48 or decimal 0.02083. The prime factors of 48 are <2 2 2 2 3> . The non unique factors could be 3,2*2(4), 2*3(6),2*2*3 (12), 2**4 ( 16 ), and 2*2*2*3(24) from inspection of available prime numbers and the observed sets of Babylonian factors. Like the Babylonians, one can use non unique factors and bigger chunk factors to save computations. Multiply 0.02083 by 3 for .06249 and save the integer factor 3. Multiply 0.06249 by 16 for .99984 and save the integer factor 16. The number 0.02083 is transformed by selected factors of 48 into unity and the integer factors were saved for 3*16 = 48.
For a quicker solution on the reverse sequence algorithm, the product of the selected non unique factors should equal the target number as well as the target number should be divisible by the selected factors. The non unique factors were selected from several problems, so it is possible that some factors may not apply to the problem. The order of the factors should be associative, but is seems that one large factor might preempt another or smaller factor.
The strategy that the Babylonians used for picking reducing factors for the reciprocal algorithms is not completely known. Here, the irregular reciprocal, trailing edge, and reverse sequence algorithms are lumped together to develop a general strategy for the eTCL calculator. The Babylonian regular numbers in base 60 are reducible by factors 2/3/5, but tiny digit factors would increase the number of calculations to reduce the target number. Using larger factors like decimal 60/225/400 entails fewer computations and that will speed up computations and reduce wait time. As the eTCL code stands, the calculator will cycle through a Babylonian factor list. As the list of factors passes through, each factor will get an equal one time chance. From the math problems, the scribes used each large factor multiple times until exhausted. Generally, the Babylonians avoided 7 and other prime numbers in their calculations system. For the eTCL calculator also, since prime numbers are not reducible in the algorithm unless listed, then the trailing edge algorithm and reverse sequence algorithm may stick on one of the infinite prime numbers. One supposes the Babylonians picked their target numbers for the reciprocal methods pretty carefully to avoid snarls of irreducible prime numbers. About thirty (30) factorizations are roughly the limit of the reciprocal math problems, based on the available problems and the size and length dimension of the clay tablets. Further, the reducing factor lists for the trailing edge and reverse sequence algorithms differed enough to mean that there were separate picking strategies.
Another possible strategy might be error checking and avoidance of error propagation. The trailing edge reciprocal is not solved for 5 to 30 multiplications and that is a lot of hand work for the Babylonian scribe. The fewer the calculations, the fewer errors to propagate and to correct. The reverse sequence algorithm might be a form of error checking for the reciprocal, ref Proust. Usually, the error check for reciprocation is performed at the end of the tablet, c*(1/c)=1. Is it possible here to check for inverse errors line by line?
Trailing edge solution has target number greater the one and reduction (dividing factors) factors greater than one. Trailing edge solution approaches one from above one. Logic statement { <fmod $limit $item > == 0 } is working for target numbers greater than one. Reverse sequence solution has target number less than one and multiplication and transformation factors less than one. For target numbers less than one, reverse sequence solution approaches one from below one.
What would low number reciprocals of high precision be used for? Late Babylonian tablets (300-400 C.E.) have tables of reciprocal numbers from 1/60 to 2/60 evaluated up to 8 powers of 60, (eg. decimal 0.017777,0.02,0.02083, 0.02222, and 0.026388, not all repeating decimals in base 10 or 60). ( Feynman's log Algorithm (1<N>2) might be worth looking here.) In base60 notation, examples of the reciprocal pairs would be (1_04, 56_15)(1_12, 50),(1_15, 48)(1_20, 45)(1_21, 44_26_40). In decimal notation, examples of the reciprocal pairs would be (1/60+4/3600, 0.017777, 56.25), (1/60+12/60, 0.02, 50) (1/60+15/3600, 0.02083, 48) (1/60+20/3600, 0.02222, 45)(1/60+35/3600, 0.026388, 44.4444). At least some Babylonian algorithms involve reduction of terms by factorization. Following the factorization task, 45=3*3*5, 48=2*2*2*2*2, 50=2*5*5. Although the eras were hundreds of years apart, the factors 45 and 48 were identified in the reverse sequence algorithm . Likewise, the factor 225 from the reverse sequence algorithm is 5*45. The factor 50 as N*50 was seen in the trailing edge algorithm, but not in the reverse sequence algorithm (but bear in mind the limited extant examples). The trailing edge algorithm was used to generate reciprocals of regular numbers and the reverse sequence was apparently used to check or reinflate the original trailing edge number. The research is trying to find if the factor 50 or N*50 would invalidate the reverse sequence algorithm? As near as I can tell, the generating series 5**3, 5*5*5*2, 5*5*5*2*2, 5*5*5*2*2*2 ... would never produce a trailing edge of 50 in base 60.
I can only suggest some kind of generating function for large squares or logarithms (meaning squares of 8 digits in base 60). The Babylonian square side rule is the sqrt(a) approximates (1/2) * ( target_number / trial_number_reciprocal + 1/ trial_number_reciprocal ). The Babylonian square side rule with a single trial input becomes less accurate with increasing trial_number, much greater than one and above 1000. The converse is probably true; The Babylonian square side rule with a single trial input becomes more accurate with decreasing trial_number, approaching one from above 1000. Ref. The powers of 9 and related mathematical tables from Babylon, Mathieu Ossendrijver (Humboldt University, Berlin)
| table 1 | observed factors et al for trailing edge algorithm | printed in | tcl wiki format | |
|---|---|---|---|---|
| calculation | factor | inverse factor | prime factors | comment, if any |
| 2 | 200 | 0.005 | 2 2 2 5 5 | |
| 3 | 400 | 0.0025 | 2 2 2 2 5 5 | |
| 4 | 10 | 0.1 | 2 5 | |
| 5 | 16 | 0.0625 | 2 2 2 2 | |
| 6 | 25 | 0.04 | 5 5 | |
| 7 | 40 | 0.025 | 2 2 2 5 | |
| 8 | 1350 | 0.0007407407407407407 | 2 3 3 3 5 5 | |
| 9 | 2 | 0.5 | 2 | added from prime number series |
| 10 | 3 | 0.3333333333333333 | 3 | added from prime number series |
| 11 | 5 | 0.2 | 5 | added from prime number series |
| table mostly from Interpretation of reverse algorithms, Christine Proust | factors above have some uncertaincy because B. notation is relative value, does not give magnitude or absolute value |
| table 2 | observed factors et al for reverse sequence algorithm | printed in | tcl wiki format | |
|---|---|---|---|---|
| calculation | factor | inverse factor | prime factors | comment, if any |
| 2 | 30 | 0.03333333333333333 | 2 3 5 | 30/60 = 1/2 |
| 3 | 12 | 0.08333333333333333 | 2 2 3 | 12/60 = 1/5 |
| 4 | 15 | 0.06666666666666667 | 3 5 | 15/60 = 1/4 |
| 5 | 24 | 0.041666666666666664 | 2 2 2 3 | 24/60 = 2/5 |
| 6 | 36 | 0.027777777777777776 | 2 2 3 3 | 36/60 = 3/5 |
| 7 | 45 | 0.022222222222222223 | 3 3 5 | 45/60 = 9/12 = 3/4 |
| 8 | 48 | 0.020833333333333332 | 2 2 2 2 3 | 48/68 = 4/5 |
| 9 | 225 | 0.0044444444444444444 | 3 3 5 5 | 225/60 = 45/12 |
| 10 | 2 | 0.5 | 2 | 2/60 = 1/30, added from prime number series |
| 11 | 3 | 0.3333333333333333 | 3 | 3/60 = 1/20, added from prime number series |
| 12 | 5 | 0.2 | 5 | 5/60 = 1/12, added from prime number series |
| table mostly from Interpretation of reverse algorithms, Christine Proust | factors above have some uncertaincy because B. notation is relative value, does not give magnitude or absolute value |
Pseudocode Section
# using pseudocode for Babylonian trailing edge algorithm
# and reverse sequence algorithm for reciprocals
# possible problem instances include, given n , find 1/n from trailing edge factors
# reverse sequence algorithm is finding inverse or 1/(1/n)
# irregular defined as not in standard B. table of reciprocals
target_number= supplied value
# decompose target number
c = a + b
1/n = (1/n1) * (1/n2)
a+b is not unique,
test a for prime, even, odd?
test b for prime, even, odd?
find a as factorable into 2**x, 3**y, 5**z, or n/<(2**x)*(3**y)*(5**z)>???
take (1/a)
table lookup (1/a)
take (1/a)*(b)
take 1/(1+(1/a)*(b))
take (1/a)* (1/(1+(1/a)*(b)))
check_answer new area =? desired goal
n*(1/n) =? 1 , (yes/no logic)
set answers and printout with resulting values
13500 >>> factors 2 2 3 3 3 5 5 5
1./13500. = 7.4074e-5
1./7.4074e-5 = 13500.
factors for 13500 or standing reciprocal algorithm on its head
2 2 3 3 3 5 5 5 *(1/5)
2 2 3 3 3 5 5 *(1/5)
2 2 3 3 3 5 *(1/5)
2 2 3 3 3 *(1/3)
2 2 3 3 *(1/3)
2 2 3 *(1/3)
2 2 *(1/2)
2
2 *(2)
2 2 *(3)
2 2 3 *(3)
2 2 3 3 *(3)
2 2 3 3 3 *(5)
2 2 3 3 3 5 *(5)
2 2 3 3 3 5 5 *(5)
2 2 3 3 3 5 5 5
set list_factors_trailing <200 400 10 16 25 40 1350> base 60
set list_factors_reverse < 30 12 15 24 36 45 48 225> base 60
# should swap out tiny prime factors for larger Babylonian factors
# if factor r does not work or is exhausted ,
# factor r should be temporally struck from the factor list.
# factor of target number on left
# factor of the reciprocal on the right
# preclean list of possible factors that do not evenly divide!
[ list_cleaner_factors $lister $item ]
# begin factorization of precleaned list of factors
# there might be factors used once or multiple times before exhausted Revamp test, using pseudocode in alternate format
# pseudocode in alternate format
# using pseudocode for Babylonian trailing edge algorithm
# and reverse sequence algorithm for reciprocals
# possible problem instances include, given n , find 1/n from trailing edge factors
# reverse sequence algorithm is finding inverse or 1/(1/n)
# irregular defined as not in standard B. table of reciprocals:
1. Initialize target_number as the supplied value
2. Decompose target_number into two factors: a and b such that c = a + b
3. Test a for being prime, even, or odd
4. Test b for being prime, even, or odd
5. Find a as factorable into 2^x, 3^y, 5^z, or n/<(2^x)*(3^y)*(5^z)>
6. Lookup (1/a) in a table and store the result
7. Calculate (1/a) * b and store the result
8. Calculate 1/(1 + (1/a) * b) and store the result
9. Calculate (1/a) * (1/(1 + (1/a) * b)) and store the result
10. Check the answer against the desired goal n * (1/n) = 1 using yes/no logic
11. Set answers and print out the resulting values
Testcases:
# For target_number = 13500:
# Factors: 2 2 3 3 3 5 5 5
# 1/13500 = 7.4074e-5
# 1/7.4074e-5 = 13500
For target_number = 13500:
Factors: 2 2 3 3 3 5 5 5
1/13500 = 7.4074e-5
1/7.4074e-5 = 13500Pseudocode Definitions of Terms and Concepts.
The Babylonian Trailing Edge Reciprocal Algorithm is an ancient algorithm used to find the reciprocal of a number by successively doubling the number and adding it to the target number. The Babylonian Reverse Sequence Reciprocal Algorithm is an algorithm for finding the inverse or 1/(1/n) of a given number. A factor is a number that divides another number without leaving a remainder. Table Lookup is a method to find a value in a pre-computed table to speed up calculations. Primality is a property of a number to be divisible only by itself and 1. Evenness is a property of a number to be divisible by 2. Oddness is a property of a number to not be divisible by 2. A reciprocal is the inverse of a number, obtained by dividing 1 by the original number. For example, the reciprocal of 2 is 1/2 or 0.5, and the reciprocal of 7 is 1/7 or approximately 0.143. In the context of the pseudocode provided, the algorithm aims to find the reciprocal of a given number by decomposing it into factors and using table lookups for speed.
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
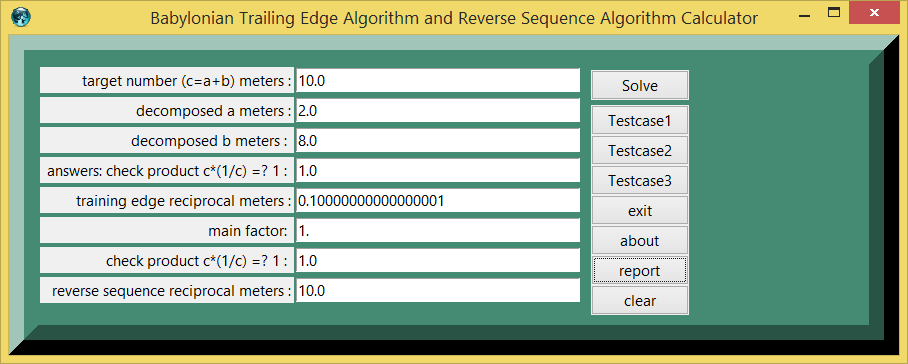
Testcase 1 for decimal 10, base10
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 10.0 : | target number (c=a+b) meters | |
| 2.0 : | decomposed a meters | |
| 8.0 : | decomposed b meters | |
| 1.0 : | answers: check product c*(1/c) =? 1 | |
| 0.100 : | reciprocal meters | |
| 1. : | main factor | |
| 1.0 : | check product c*(1/c) =? 1 | |
| 10.0 : | reverse sequence reciprocal meters |
Testcase 2 for decimal 20, base10
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 20.0 : | target number (c=a+b) meters | |
| 4.0 : | decomposed a meters | |
| 16.0 : | decomposed b meters | |
| 1.0 : | answers: check product c*(1/c) =? 1 | |
| 0.050 : | reciprocal meters | |
| 1. : | main factor | |
| 1.0 : | check product c*(1/c) =? 1 | |
| 20.0 : | reverse sequence reciprocal meters |
Testcase 3 for decimal 5, base10
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 5.0 : | target number (c=a+b) meters | |
| 2.0 : | decomposed a meters | |
| 3.0 : | decomposed b meters | |
| 1.0 : | answers: check product c*(1/c) =? 1 | |
| 0.200 : | reciprocal meters | |
| 1. : | main factor | |
| 1.0 : | check product c*(1/c) =? 1 | |
| 5.0 : | reverse sequence reciprocal meters |
Testcase 4 for decimal 525, base10
| table 4 | printed in | tcl wiki format | trailing edge algorithm for decimal 525 | |
|---|---|---|---|---|
| quantity | value | factor | comment, if any | |
| calculation | reduction of target number | factor | tracking reciprocal solution | |
| counter | target number | division factor | inverse factor | developing product of reciprocal factors |
| 1 | 525 | 5 | 1/5 | (1/5) |
| 2 | 105 | 5 | 1/5 | (1/5) *(1/5 ) |
| 3 | 21 | 7 | 1/7 | (1/5) *1/5) * (1/7) |
| 4 | 3 | 3 | 1/3 | (1/5) *(1/5)* (1/7) * (1/3) |
| 5 | 1 | 1 | 0.0019 | target reduction to one and final value of reciprocal |
set answer2 [expr {(1./5.) *(1./5.)* (1./7.) * (1/3.) }]
# answer 0.00190476190476190
tcl_prime_factors (525) = 3 5 5 7 Testcase 5 for decimal 21600, base10
| table 5 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 21600.0 : | target number (c=a+b) meters | |
| 20.0 : | decomposed a meters | |
| 21580.0 : | decomposed b meters | |
| 1.0 : | answers: check product c*(1/c) =? 1 | |
| 4.6296e-05 : | reciprocal meters | |
| 1. : | main factor | |
| 0.9999 : | check product c*(1/c) =? 1 | |
| 21599.9999 : | inverse reciprocal ( reverse sequence ) meters |
tcl_prime_factors (21600) <2 2 2 2 2 2 3 3 3 5 5 5>.
[expr (1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./3.)*(1./3.)*(1./3.)*(1./5.)*(1./5.)*(1./5.)]
answer 4.62962962962963e-6Testcase 6 for decimal 1296000., base10
| table 6 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 12960000.0 : | target number (c=a+b) meters | |
| 20.0 : | decomposed a meters | |
| 12959980.0 : | decomposed b meters | |
| 1.0 : | answers: check product c*(1/c) =? 1 | |
| 7.7160493827160495e-08 : | reciprocal meters | |
| 1. : | main factor | |
| 1.0 : | check product c*(1/c) =? 1 | |
| 12960000.0 : | inverse reciprocal ( reverse sequence ) meters |
tcl_prime_factors (12960000) < 2 2 2 2 2 2 2 2 3 3 3 3 5 5 5 5 >.
[expr (1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./2.)*(1./3.)*(1./3.)*(1./3.)*(1./3.)*(1./5.)*(1./5.)*(1./5.)*(1./5.)]
reciprocal = 7.716049382716051e-8
Screenshots Section
figure 1.
References:
- Interpretation of reverse algorithms in several mesopotamian texts, Christine Proust
- A Geometric Algorithm with Solutions to Quadratic Equations
- in a Sumerian Juridical Document from Ur III Umma
- Joran Friberg, Chalmers University of Technology, Gothenburg, Sweden
- google search engine <Trapezoid area bisection>
- Wikipedia search engine <Trapezoid area >
- mathworld.wolfram.com, Trapezoid and right trapezoid
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
- www.britannica.com, topic, mathematics trapezoid
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Babylonians Tracked Jupiter With Advanced Tools: Trapezoids, Michael Greshko, news.nationalgeographic.com
- Geometry in Babylonian Astronomy, Cluster of Excellence Topology, Humboldt University of Berlin
- Mathieu Ossendrijver: „Ancient Babylonian astronomers calculated Jupiter’s position
- from the area under a time-velocity graph“, in: Science, January 29, 2016.
- Late Babylonian Field Plans in the British Museum, books.google.com/books
- Karen Rhea Nemet-Nejat
- Late Babylonian Surface Mensuration Author(s): Marvin A. Powell Source: jstor
- translation: trapezoid in two babylonian astronomical cuneiform
- texts for jupiter (act 813 & act 817) from the seleucid era , 310 BC -75 AD
- Otto Neugebauer, Astronomical Cuneiform Texts, 3 Vols.
- Lund Humphreys, London, 1955:405,430-31.
- DeSegnac, MS 3908 A RE-CONSTRUCTION, D.A.R. DeSegnac
- A draft for an essay
- DeSegnac, MENTAL COMPUTING OF THREE ARCHAIC
- MESOPOTAMIAN PUZZLES W 20044, 35, W 20044, 20 & W 20214, essay draft
- DeSegnac, HARMONY OF NUMBERS I and II, D.A.R. DeSegnac, A draft for an essay
- Asger Aaboe, Some Seleucid Mathematical Tables
- (Extended Reciprocals and Squares of Regular Numbers)
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Trailing Edge Algorithm and Reverse Sequence Algorithm Calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and 1.0.1
# gold on TCL WIKI, 25jan2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { regular integer number (c=a+b, c>1) meters :} }
lappend names { optional, decomposed a meters :}
lappend names { optional, decomposed b meters : }
lappend names { answers: check product c*(1/c) =? 1 : }
lappend names { training edge reciprocal meters :}
lappend names { possible reverse sequence factors, non unique: }
lappend names { check product c*(1/c) =? 1 : }
lappend names { inverse reciprocal ( reverse sequence ) meters :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Trailing Edge Algorithm and Reverse Sequence Algorithm
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc listcleaner {target args} {
set res $target
foreach unwant $args {
# suchenworth idea
set res [lsearch -all -inline -not -exact $res $unwant ]
}
return $res
}
proc doubling_halving_algorithm { target_number } {
global side1 side2 side3 side4 side5
global side6 side7 side8
global doubling_halving_reciprocal check_answer_product4
# initialize placeholder answer
set doubling_halving_reciprocal 1.
set target_a 2
set reciprocal .5
set doubling_halving_reciprocal [* [/ $target_a $target_number ] $reciprocal ]
puts "doubling_halving $doubling_halving_reciprocal "
return $doubling_halving_reciprocal
}
proc irregular_reciprocal_algorithm { target_number decom_a decom_b } {
global side1 side2 side3 side4 side5
global side6 side7 side8
global irregular_reciprocal check_answer_product3
set term1 1
set term2 1
# initialize placeholder answer
set irregular_reciprocal 1.
catch {set term1 [* [/ 1. $decom_a ] $decom_b ]}
set term2 [/ 1. [+ 1. $term1 ]]
set irregular_reciprocal [* [/ 1. $decom_a ] $term2 ]
# product $target_number * irregular_reciprocal should equal one
set check_answer_product [* $target_number $irregular_reciprocal ]
# check for lazy entries of zero, revert to modern way of reciprocals
if { $side2 < .00001 } { set reciprocal [/ 1. $target_number ] }
if { $side3 < .00001 } { set reciprocal [/ 1. $target_number ] }
if { $side2 < .00001 } { set check_answer_product [* $target_number $reciprocal ] }
if { $side3 < .00001 } { set check_answer_product [* $target_number $reciprocal ] }
set check_answer_product3 $check_answer_product
return irregular_reciprocal
}
proc reverse_sequence_reciprocal {limit } {
global counter
global list_factors_trailing list_factors_reverse lister
set counter 1
set comp 1
# base 10
set lister { 2 3 5 }
set inverse 1.
puts "%|table 2|printed in| tcl wiki format| trailing edge algorithm |% "
puts "&| quantity| value| factor |comment, if any|&"
puts "&| calculation |reduction of target number | factor | tracking reciprocal solution |&"
puts "&| counter | limit | item | inverse |&"
# base 60, Babylonians used larger factors for fewer calculations
set list_factors_trailing {200 400 10 16 25 40 1350}
set list_factors_reverse { 30 12 15 24 36 45 48 225}
set lister { 30 12 15 24 36 45 48 2 3 5 }
# should swap out tiny prime factors for larger Babylonian factors
# preclean list of possible factors that do not evenly divide!
# begin factorization of precleaned list of factors
# there might be factors used once or multiple times before exhausted
while { $counter < 50. } {
foreach item $lister {
if { [fmod [/ 1. $limit ] [/ 60. $item ] ] == 0 } {
set limit [* $limit [/ 60. $item ] ];
incr comp ;
set inverse [* $inverse [/ 60. $item ] ] }
puts "&| $comp | $limit | $item | $inverse |&"
if { $limit > .99999 } { return $inverse }
}
incr counter
} }
proc trailing_edge_reciprocal {limit } {
global counter
global list_factors_trailing list_factors_reverse lister
set counter 1
set comp 1
# base 10
set lister { 2 3 5 }
set inverse 1.
puts "%|table 2|printed in| tcl wiki format| trailing edge algorithm |% "
puts "&| quantity| value| factor |comment, if any|&"
puts "&| calculation |reduction of target number | factor | tracking reciprocal solution |&"
puts "&| counter | limit | item | inverse |&"
# base 60, Babylonians used larger factors for fewer calculations
set list_factors_trailing {200 400 10 16 25 40 1350}
set list_factors_reverse { 30 12 15 24 36 45 48 225}
set lister { 30 12 15 24 36 45 48 225 2 3 5 }
# should swap out tiny prime factors for larger Babylonian factors
# preclean list of possible factors that do not evenly divide!
foreach item $lister {
if { [fmod $limit $item ] != 0 } { set lister [ listcleaner $lister $item ] }
# puts " $lister " # used for report of cleaning exhausted factors
}
# begin factorization of precleaned list of factors
# there might be factors used once or multiple times before exhausted
while { $counter < 50. } {
foreach item $lister {
if { [fmod $limit $item ] == 0 } {
set limit [/ $limit $item ] ;
incr comp ;
set inverse [* $inverse [/ 1. $item ]] }
if { [fmod $limit $item ] != 0 } { set lister [ listcleaner $lister $item ] }
puts "&| $comp | $limit | $item | $inverse |&"
if { [/ $limit 1 ] == 1 } { return $inverse }
}
incr counter
} }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global list_factors_trailing list_factors_reverse lister
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set side1 [* [int $side1 ] 1. ]
if { $side1 < 1. } {set side1 1.}
set target_number $side1
set decom_a $side2
set decom_b $side3
# note: non unique decom_a and decom_b are
# used as breakpoints in some Babylonian
# math problems on reciprocals, but not all problems
# decom_a + decom_b = target_number
# initialize placeholder answer
set reciprocal 1.
# begin doubling_halving_algorithm
set doubling_halving_reciprocal [ doubling_halving_algorithm $target_number ]
# begin irregular_reciprocal_algorithm
set irregular_reciprocal_result [ irregular_reciprocal_algorithm $target_number $decom_a $decom_b ]
# begin trailing_edge_algorithm
set trailing_edge_result [ trailing_edge_reciprocal $target_number ]
# begin reverse_sequence_algorithm
set reverse_sequence_result [ reverse_sequence_reciprocal $trailing_edge_result]
catch {set check_answer_product1 [* 1. $target_number $trailing_edge_result ] }
catch {set check_answer_product2 [* 1. $trailing_edge_result $reverse_sequence_result ] }
catch { set side4 $check_answer_product1 }
set side5 $trailing_edge_result
set side6 $list_factors_reverse
catch { set side7 $check_answer_product2 }
set side8 $reverse_sequence_result
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number reference_factor flag
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|regular integer number (c=a+b, c>1) | |&"
puts "&| $side2 :|decomposed a meters | |& "
puts "&| $side3 :|decomposed b meters | |& "
puts "&| $side4 :|answers: check product c*(1/c) =? 1| |&"
puts "&| $side5 :|trailing edge reciprocal meters | |&"
puts "&| $side6 :|possible reverse sequence factors, non unique | |&"
puts "&| $side7 :|check product c*(1/c) =? 1 | |&"
puts "&| $side8 :|inverse reciprocal ( reverse sequence ) meters | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command {set side6 1.; calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 10. 2. 8.0 1. 1. 1. 1. 0.1}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 20. 4.0 16. 1. 1. 1. 1. .05 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 5. 2.0 3.0 1. 1. 1. 1. .2 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Trailing Edge Algorithm and Reverse Sequence Algorithm Calculator" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program under test.
# autoindent from ased editor
# console program for inverse reciprocal
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 28jan2017
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc factor_num {num} {
# subroutine by MS from Sample Math Programs
for {set i 2} {$i <= $num} {} {
if {![expr {$num % $i}]} {
lappend factors $i
set num [expr {$num / $i}]
} elseif {[expr $i*$i > $num]} {
lappend factors $num
break
} elseif {$i != 2} {
incr i 2
} else {
set i 3
}
}
return $factors
}
# priority trailing edge factors from Base 60 tablets
set list_factors_trailing [ 200 400 10 16 25 40 1350 ]
set list_factors_reverse [ 30 12 15 24 36 45 48 225 ]
# should swap out tiny prime factors for larger Babylonian factors
set inverse 1.
foreach item [ factor_num 13500 ] {
set inverse [* $inverse [/ 1. $item ]]
}
# if { ::math::decimal::remainder { a b } =< 0 } { then number is evenly divisible by a }
# if { [/ $n $i] == 0} { lappend factors $i [expr {$n / $i}] }
puts "12709 [ factor_num 12709] 13500 [ factor_num 13500 ] "
puts " $inverse " output
12709 71 179 13500 2 2 3 3 3 5 5 5
7.4074074074074087e-05 Console program for trailing edge reciprocal algorithm
# autoindent from ased editor
# console program for trailing edge reciprocal algorithm
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 30jan2017
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
proc listcleaner {target args} {
set res $target
foreach unwant $args {
# suchenworth idea
set res [lsearch -all -inline -not -exact $res $unwant ]
}
return $res
}
proc inverseit {limit } {
global counter
set counter 1
set comp 1
# base 10
set lister { 2 3 5 }
set inverse 1.
puts "%|table 2|printed in| tcl wiki format| trailing edge algorithm |% "
puts "&| quantity| value| factor |comment, if any|&"
puts "&| calculation |reduction of target number | factor | tracking reciprocal solution |&"
puts "&| counter | limit | item | inverse |&"
# base 60, Babylonians used larger factors for fewer calculations
set list_factors_trailing {200 400 10 16 25 40 1350}
set list_factors_reverse { 30 12 15 24 36 45 48 225}
set lister { 30 12 15 24 36 45 48 225 2 3 5 }
# should swap out tiny prime factors for larger Babylonian factors
# preclean list of possible factors that do not evenly divide!
foreach item $lister {
if { [fmod $limit $item ] != 0 } { set lister [ listcleaner $lister $item ] }
puts " $lister "
}
# begin factorization of precleaned list of factors
# there might be factors used once or multiple times before exhausted
while { $counter < 50. } {
foreach item $lister {
if { [fmod $limit $item ] == 0 } {set limit [/ $limit $item ] ; incr comp ; set inverse [* $inverse [/ 1. $item ]] }
if { [fmod $limit $item ] != 0 } { set lister [ listcleaner $lister $item ] }
puts "&| $comp | $limit | $item | $inverse |&"
if { [/ $limit 1 ] == 1 } { return $inverse }
}
incr counter
} }
puts "&| [ inverseit 13500 ] | answer for reciprocal |||& " output 2
| table 2 | printed in | tcl wiki format | trailing edge algorithm |
|---|---|---|---|
| quantity | value | factor | comment, if any |
| calculation | reduction of target number | factor | tracking reciprocal solution |
| counter | limit | item | inverse |
| 2 | 450 | 30 | 0.03333333333333333 |
| 2 | 450 | 12 | 0.03333333333333333 |
| 3 | 30 | 15 | 0.0022222222222222222 |
| 3 | 30 | 36 | 0.0022222222222222222 |
| 3 | 30 | 45 | 0.0022222222222222222 |
| 3 | 30 | 225 | 0.0022222222222222222 |
| 4 | 15 | 2 | 0.0011111111111111111 |
| 5 | 5 | 3 | 0.00037037037037037035 |
| 6 | 1 | 5 | 7.407407407407407e-5 |
| 7.407407407407407e-5 | answer for reciprocal |
| table 3 | printed in | tcl wiki format | reverse sequence algorithm |
|---|---|---|---|
| quantity | value | factor | comment, if any |
| calculation | reduction of target number | factor | tracking reciprocal solution |
| counter | limit | item | inverse |
| 2 | 4500 | 30 | 0.03333333333333333 |
| 3 | 375 | 12 | 0.0027777777777777775 |
| 4 | 25 | 15 | 0.00018518518518518515 |
| 4 | 25 | 24 | 0.00018518518518518515 |
| 4 | 25 | 36 | 0.00018518518518518515 |
| 4 | 25 | 45 | 0.00018518518518518515 |
| 4 | 25 | 225 | 0.00018518518518518515 |
| 4 | 25 | 2 | 0.00018518518518518515 |
| 4 | 25 | 3 | 0.00018518518518518515 |
| 5 | 5 | 5 | 3.703703703703703e-5 |
| 5 | 5 | 30 | 3.703703703703703e-5 |
| 6 | 1 | 5 | 7.407407407407407e-6 |
| 7.407407407407407e-6 | answer for reciprocal |
Console program for reverse_sequence_reciprocal algorithm
# autoindent from ased editor
# console program for reverse sequence reciprocal algorithm
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 30jan2017
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
proc reverse_sequence_reciprocal {limit } {
global counter
set counter 1
set comp 1
# base 10
set lister { 2 3 5 }
set inverse 1.
puts "%|table 2|printed in| tcl wiki format| trailing edge algorithm |% "
puts "&| quantity| value| factor |comment, if any|&"
puts "&| calculation |reduction of target number | factor | tracking reciprocal solution |&"
puts "&| counter | limit | item | inverse |&"
# base 60, Babylonians used larger factors for fewer calculations
set list_factors_trailing {200 400 10 16 25 40 1350}
set list_factors_reverse { 30 12 15 24 36 45 48 225}
set lister { 30 12 15 24 36 45 48 2 3 5 }
# should swap out tiny prime factors for larger Babylonian factors
# preclean list of possible factors that do not evenly divide!
# begin factorization of precleaned list of factors
# there might be factors used once or multiple times before exhausted
while { $counter < 50. } {
foreach item $lister {
#set item [/ $item 60. ]
#if { [fmod $limit $item ] == 0 } {set limit [* $limit [/ 60. $item ] ]; incr comp ; set inverse [* $inverse $item ] }
if { [fmod [/ 1. $limit ] [/ 60. $item ] ] == 0 } {set limit [* $limit [/ 60. $item ] ]; incr comp ; set inverse [* $inverse [/ 60. $item ] ] }
#if { [fmod $limit $item ] != 0 } { set lister [ listcleaner $lister $item ] }
puts "&| $comp | $limit | $item | $inverse |&"
if { $limit > .99999 } { return $inverse }
}
incr counter
} }
puts "&| [ reverse_sequence_reciprocal .001 ] | answer for reciprocal |||& "
| reverse_sequence_reciprocal algorithm | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | factor | comment, if any |
| calculation | reduction of target number | factor | tracking reciprocal solution |
| counter | limit | item | inverse |
| 2 | 0.002 | 30 | 2.0 |
| 3 | 0.01 | 12 | 10.0 |
| 4 | 0.04 | 15 | 40.0 |
| 5 | 0.1 | 24 | 100.0 |
| 5 | 0.1 | 36 | 100.0 |
| 5 | 0.1 | 45 | 100.0 |
| 6 | 0.125 | 48 | 125.0 |
| 6 | 0.125 | 2 | 125.0 |
| 6 | 0.125 | 3 | 125.0 |
| 6 | 0.125 | 5 | 125.0 |
| 7 | 0.25 | 30 | 250.0 |
| 7 | 0.25 | 12 | 250.0 |
| 8 | 1.0 | 15 | 1000.0 |
| 1000.0 | answer for reciprocal |
gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |