Gauss Approximate Number of Primes and eTCL demo example calculator
Gauss Approximate Number of Primes and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Gauss Approximate Number of Primes and eTCL demo example calculator, numerical analysis
- Introduction
- Gauss approximation
- Legendre and Modified_Legendre approximations
- Devil's notch in Pcf(x)
- Ribeiro approximation and extensions
- Riemann fluctuations in prime counting function
- Old_Newsflash
- Legendre correction constant using TCLLIB prime functions in TCLLIB
- Subject: consider prime numbers as fish in a vast sea, TCL programming
- One Liner programs on Primes, Twin Primes, and Primes separated by Even Numbers
- Summary
- Table Results on Twin Primes for 2,4,6,10 Separators
- 2021 Newsflash, TCLLIB has twin primes and cousin primes routines in TCLLIB:math ticket pipeline
- Prime Difference Function
- Table: Prime Difference Function
- Table: Rarity of Primes as percent reported from Modified_Legendre_primes function
- Appendix Code
- appendix TCL programs and scripts
- Pushbutton Operation
- Console program used to build csv spreadsheet charts.
- Console program for devil's notch
- Alternate Console programs for prime_counting_function
- Console program for sum of reciprocal squares of prime numbers.
- Table for prime_zeta_function
- References:
- Credits on One Liner Programs
- Comments Section
Introduction
gold Here are some eTCL starter code for Gauss approximate number of primes. The impetus for these calculations was checking approximations for the Riemann theorem. Most of the testcases involve assumptions and rules of thumb. Npte: Some tickets are closed and functions available in Tcllib. Many thanks to arjen & Andreas Kupries for the heavy lifting.
Not a Replacement for TCL Core
gold Update 3/2/2024. This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
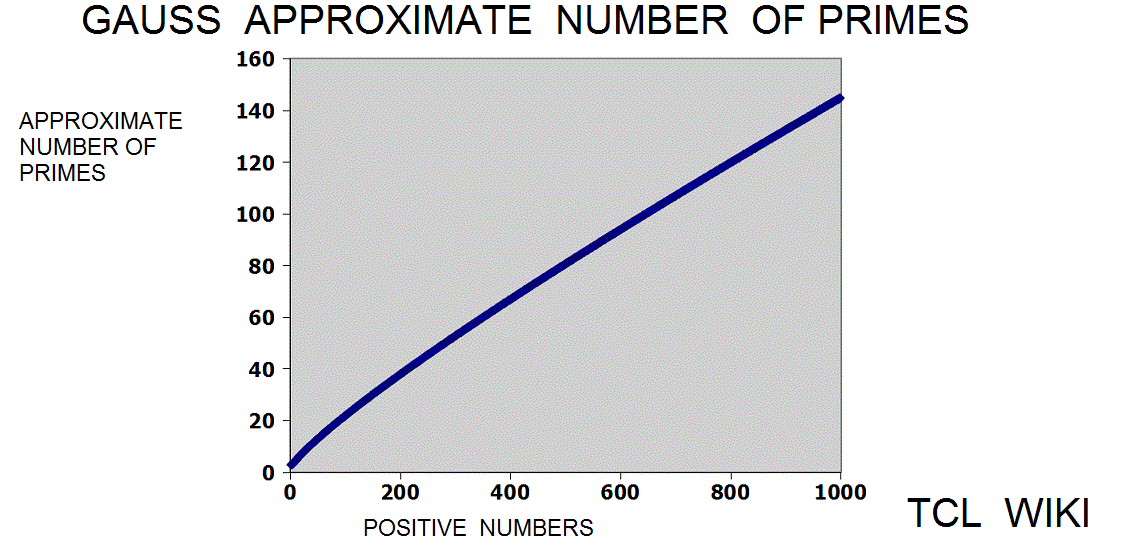
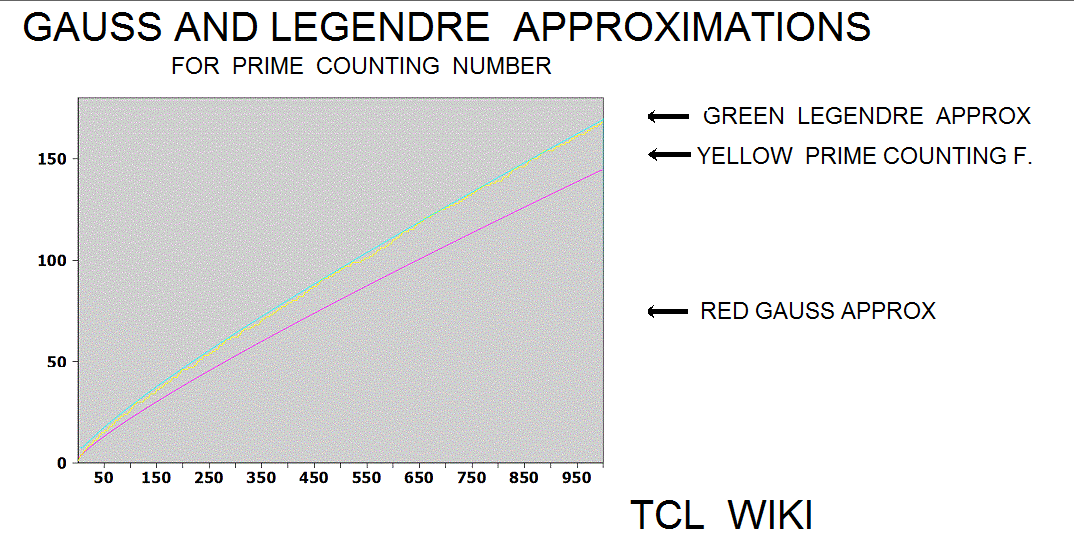
Gauss approximation
The Gauss approximation for number of primes is approx_number_primes = N1 / ln (N1), 15 percent average error. Gauss developed this formula at the age of 14! and formula was first published in 1863. If the exact solution is tabbed as one, the program is storing the exact solution in a list of limited size. The number one should not be counted as a prime and the number two is counted as prime, so some starting algorithm statements are tricky.
Legendre and Modified_Legendre approximations
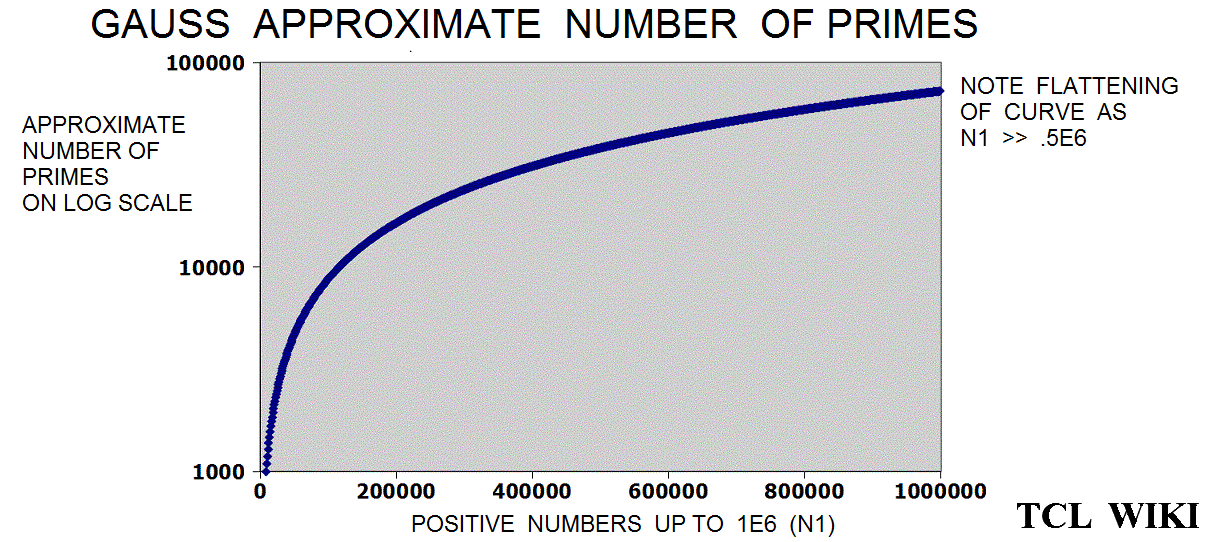
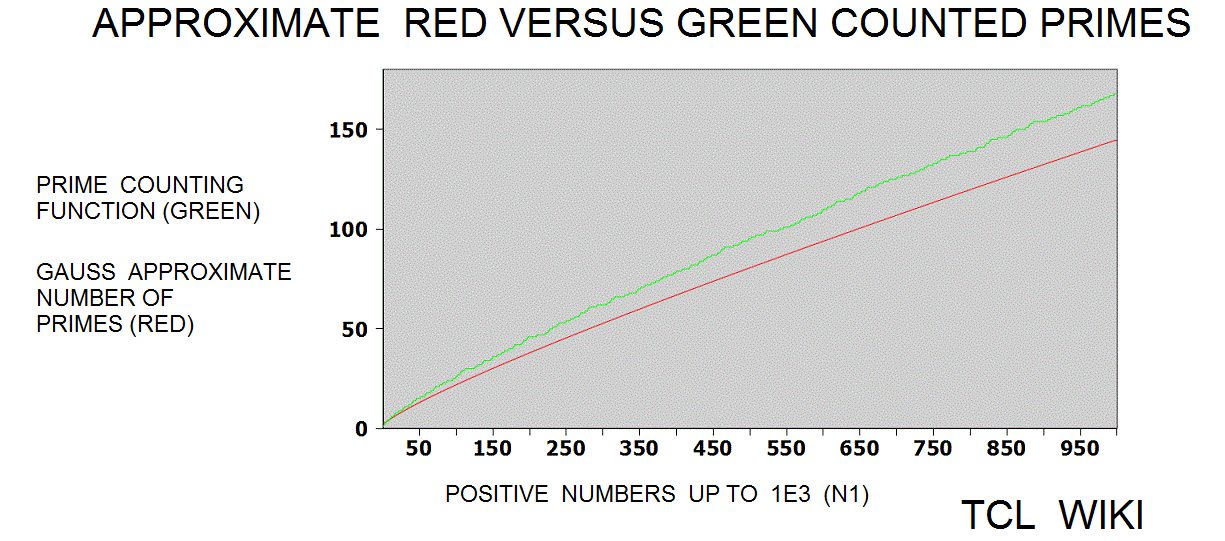
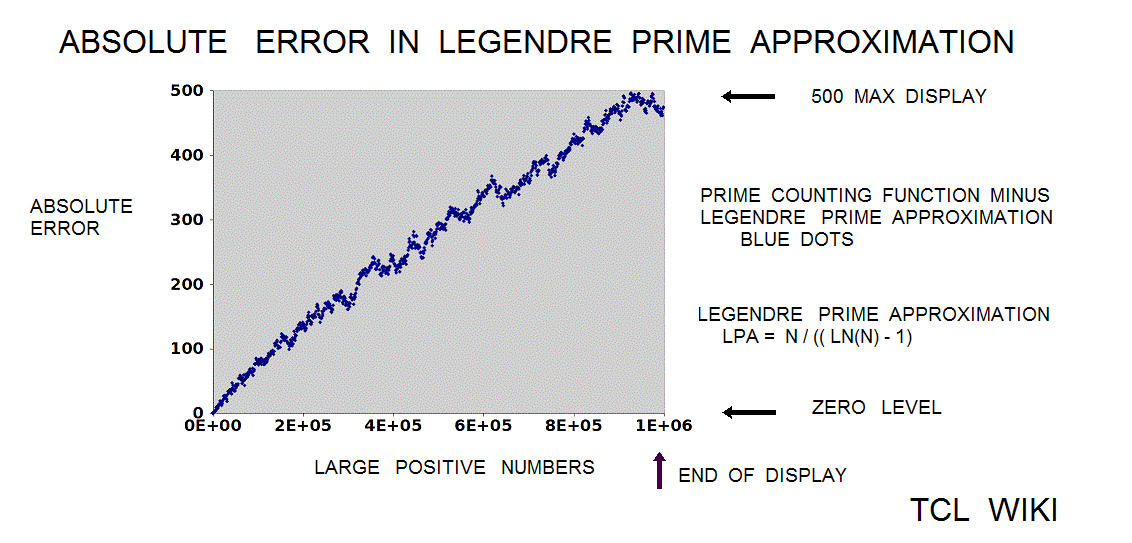
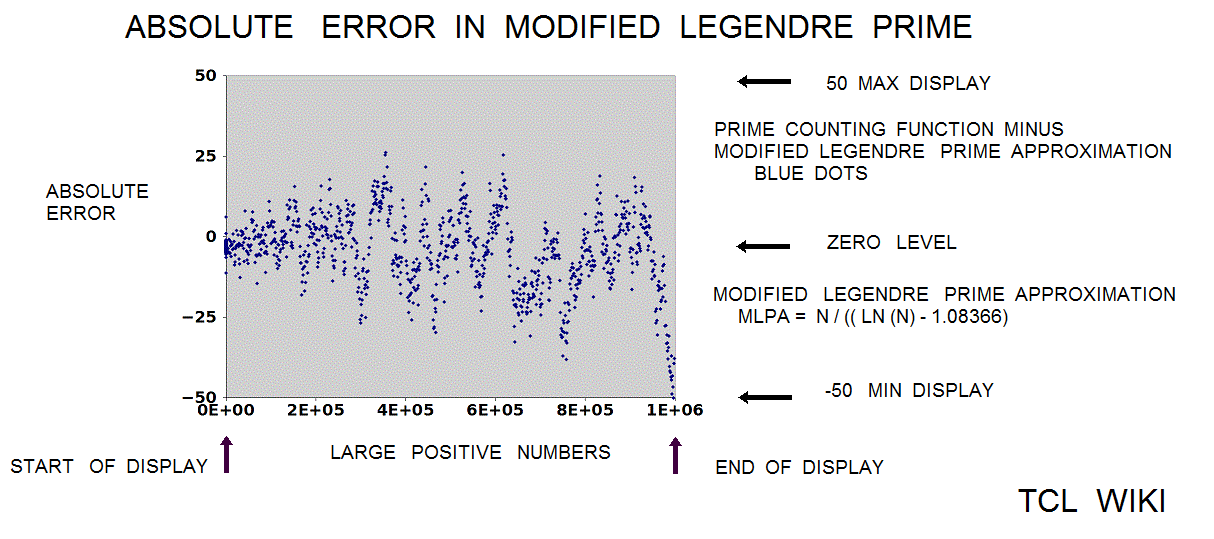
The Legendre approximation for number of primes was approx_legendre_primes2 = N1 / (ln (N1)-1), 2 percent average error beyond 1E4. A variant of the Legendre equation was modified_legendre_primes3 = N1 / (ln (N1)-1.08366). In the modified Legendre error covering E6, no particular trends are seen leading from zero level, but there are some sawtooth patterns at intervals. Also the prime counting function is reported to have gaps between the primes, which might be difficult to see at this density.
# following statements can be pasted into TCL console
set project 1.0
proc gaussian_primes {n} { return [/ $n [log $n] ] }
puts "gaussian_primes [ gaussian_primes 100 ] " # answer 21.71472409516259
proc legendre_primes2 {n} { return [/ $n [- [log $n] 1.] ] }
puts "legendre_primes2 [ legendre_primes2 100 ] " # answer 27.73794157864211
proc modified_legendre_primes3 {n} { return [/ $n [- [log $n] 1.08366] ] }
puts "modified_legendre_primes3 [ modified_legendre_primes3 100 ] " # answer 28.39690778061494
# answer 25 prime_counting_functionx for 100 is 25 # answer 25
# nth prime f(x) =~~ 1.13*log(x)
proc mod_percent {n} { set aa [/ $n [- [log $n] 1.08366] ] ;return [* [/ $aa $n ] 100. ] }
# percentage of primes at given number n from modified_legendre_primes3
# shows increasing rarity of primes as n increases beyond 1E12
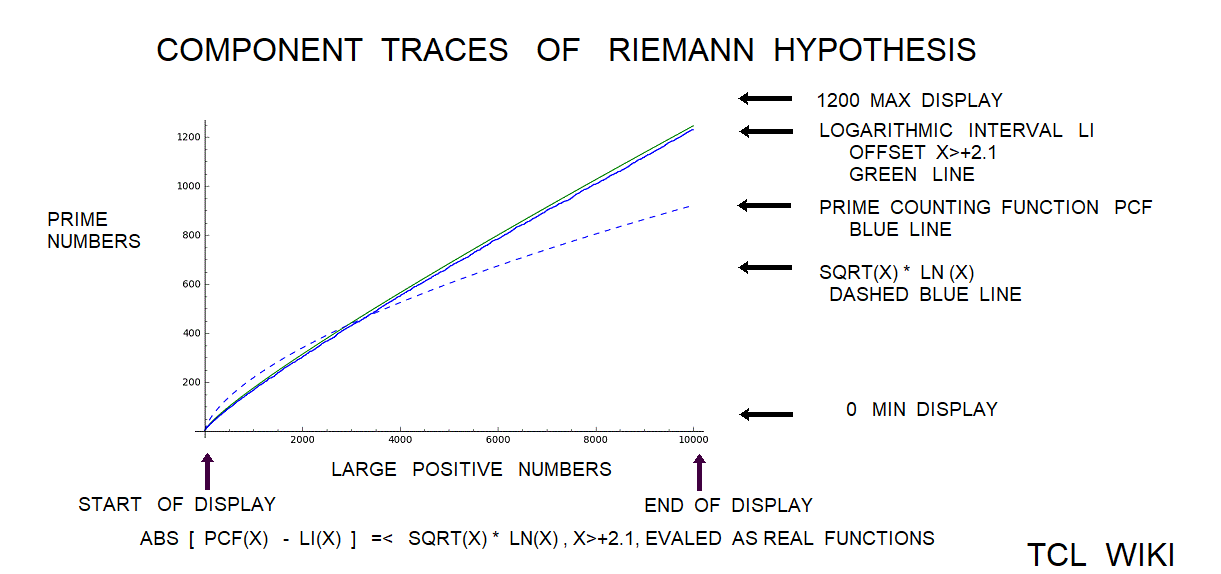
# Riemann Hypothesis Equivalent, For all x => 2.01,abs {prime_pi(x) − Li(x)} =< sqrt(x) * log(x).
# prime number theorem, Li(x)=∼~ prime_pi(x) Devil's notch in Pcf(x)
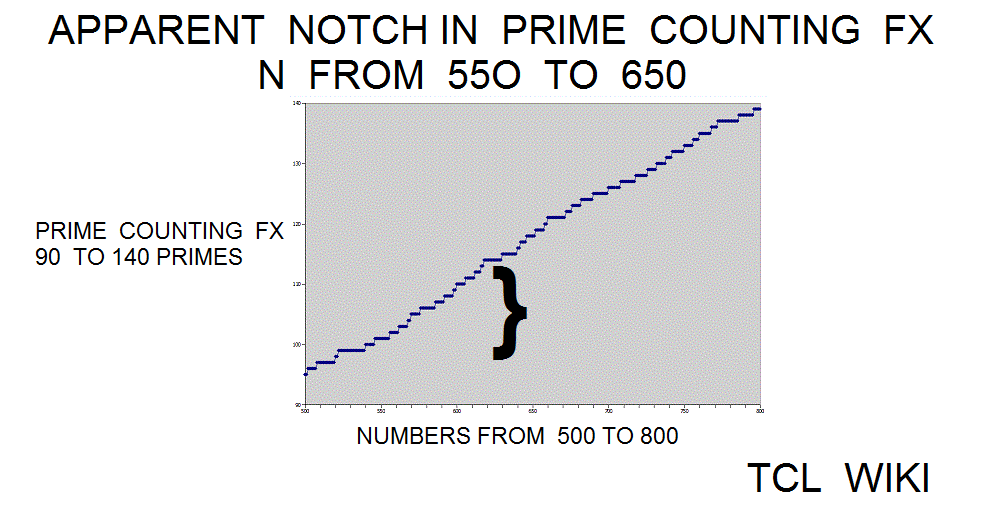
What causes the devil's notch in the prime counting function from numbers 550 to 650? This region is best seen on the graphs of the prime counting function or the difference curves between the prime counting function and the Gauss approximation. Maybe the notch is numerical coincidence in "random noise" or human misperception, but the notch can show some of the calculator uses. The calculator and some subroutines in the TCLLIB can be used to examine this region. Using the calculator in step intervals of (450 550), (550 650), and (550 650), there was a slight increase in the number of primes as steps 14,17,14. The gauss reported predictions of 13.505,13.191,12.936 primes in the notch and adjacent regions. The corrected Legendre function reported predictions of 15.696,15.281,14.947 primes in the notch and adjacent regions. The slight increase in the devil's notch goes against the general trend that primes should become more rare either in the large numbers or as N increases. The corrected Legendre function is one or two off in its prediction of prime numbers in the adjacent intervals, but the expectation from both the gauss and Legendre functions is a gentle decrease in primes, not a bump up to 17 primes. As the calculator passes through the devil's notch, the prime numbers can be gathered in a list and printed out on the console. Try inserting lappend list and put statements in the prime_counting_functionx or the calculator . The prime number 601 is in the middle of the notch and its nearest integer root is 25, if a prime number has such baggage. Hinkley's Tables of primes has similar intervals of 100 mapped out, but no answer leaped from the pages. (Other pages are reporting a gap of primes, starting at 521, which may be relevant. Might be useful to have calculator report gaps in prime numbers.)
Mathematicians have been fascinated with the many factors in 60. The number 60 is thought the beginning of a cliff of numbers with higher counts of factors or higher possibilities of factors. 60 is bounded by a set of twin primes as 59 and 61. Possibly there is something special about 60 or 60*10?
Ribeiro approximation and extensions
The Ribeiro paper models the error or correction function like the modified Legendre function. The modified Legendre function was $x/(log($x)-1.08366). Legendre was modeling the correction with a constant 1.08366. An equivalent expression for the Legendre function might be $x/(log($x) -1. -.08366) or $n/(log($n) -1. - error_fx($n)). Under consideration is a error model that uses the smaller quantity, ABS 0.08366 rather than ABS 1.08366. The Legendre function using ABS 0.08366 might allow simpler functions. The Ribeiro function starts with the setup $x/(log($x)-error_f($x)) and models the error with error_f($x) = 0.7013/$x – 4.964*exp (-0.9677*$x) + 0.98, condition that 0<+$x<10E22. The Ribeiro paper used a hand calculator or spreadsheet, effectively single precision constants. A prospective TCL procedure could be double precision TCL_17 or higher. There might be advantage in solving the error_f(x) as double precision or substituting a different modeling function with the autosolve.
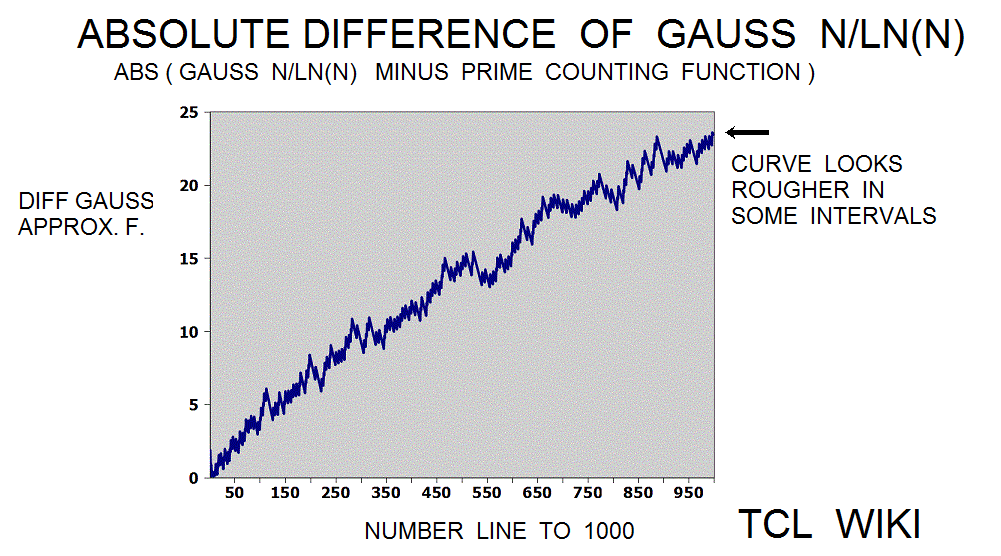
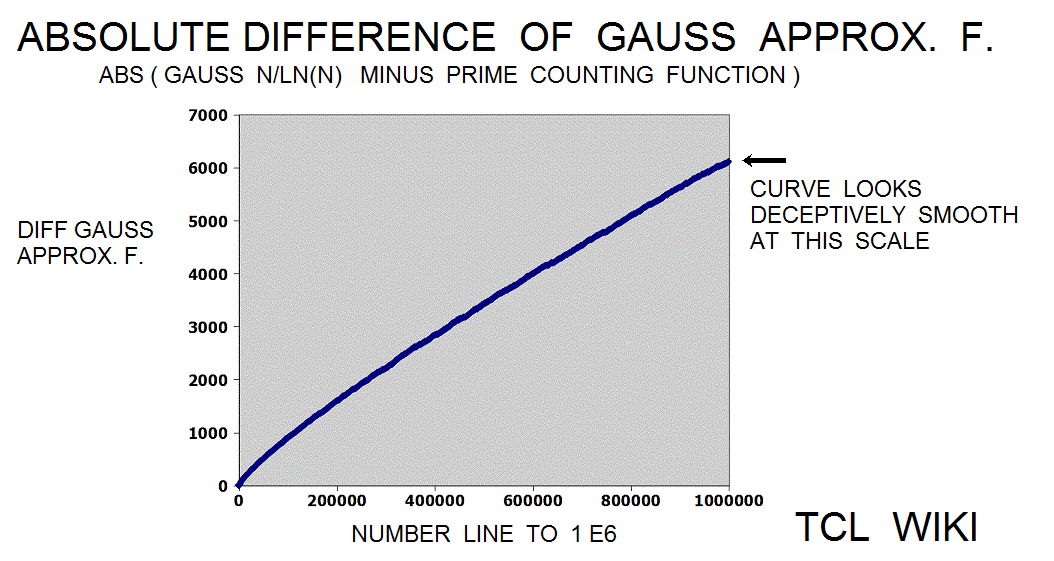
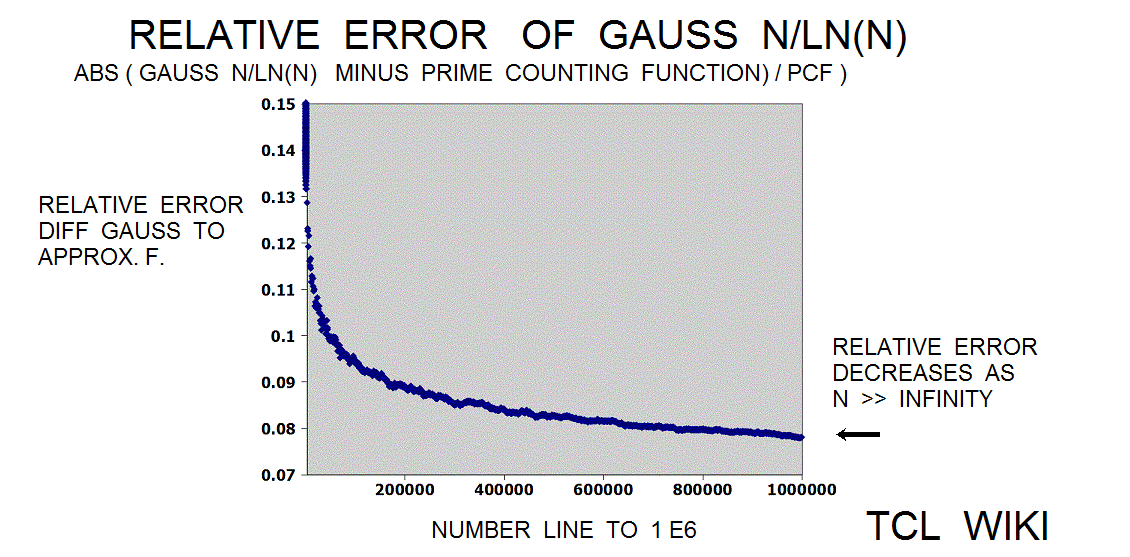
Riemann fluctuations in prime counting function
The Riemann translation mentioned periodic fluctuations past 1E5. There are periodic waves (or sawtooth ) of about 1E5 (100,000 on the number line) in a chart of the ABS(prime counting function -modified legendre approximation for pcf.) Show a graph of the prime counting function minus the modified legendre function (m. legendre error) over the interval zero to 1E6. There is no particular trend leading from zero to 1E6 , but there are sawtooth patterns in the trace at regular intervals (to the eyeball). In some computer docs, the prime counting function is called the number of primes less than. The modified Legendre prime approximation is MLPA = N/ ((LN(X)-1.08336). Essentially, the dots are the numbers of primes per number on the number line from zero to one million (1E6) with the rise or growth subtracted by the modified Legendre prime approximation (to a level trace). There are similar charts on the Wolfram system (for abs(PFC-LI)) on /mathworld.wolfram.com/PrimeCountingFunction.html and /mathworld.wolfram.com/RiemannPrimeCountingFunction.html, >except< that the chart here is zero to 1E6 and the Wolfram chart is zero to 1000. The original Riemann paper quotes periodic terms. Apparently, certain periodic terms grow past 1E5, possibly fractions and powers of li. li-1/2*li(x^(1/2))-1/3*li(x^(1/3))-1/5*li(x^(1/50)+1/6*li*(x^(1/6)) ..... Might be helpful (or too much detail ) to expand or supplement the Wolfram charts to 1E6 or 3E6, as mentioned in the Riemann paper. The periodic fluctuations are not seen much below 1E5 according to Riemann.
Old_Newsflash
gold 2017-05-28. As of May2017, the TCLLIB has developed code for numberPrimesGauss, numberPrimesGauss, and numberPrimesLegendreModified in the math::numtheory.tcl and math::primes.tcl modules. For now, this supplemental numtheory.tcl code is posted on the TCLLIB website until further core approval and distribution in the formal TCLLIB library. This math::numtheory.tcl seems really exciting work, which will keep TCL in pace with some of the other brand name languages (math oriented). These formulas are in the ball park subject of the Riemann Prime Number Theory. If one can not wait, the TCL user may download the supplemental math::numtheory code into his existing TCLLIB on his personal machine. I will not repeat not duplicate the TCLLIB code on this page.
Legendre correction constant using TCLLIB prime functions in TCLLIB
In the modified_legendre prime estimate, the correction constant of 1.08366 seemed well chosen. The analysis made some hand calculations for checking some independent constants using the primes tools in the TCLLIB, particularly primes::primesLowerThan. The primesLower function found 1229 primes in the 10K natural numbers. For 10K, the correction constant was - [log 10000. / 10000. 1229. ] or 1.073643. The primesLower function found 9592 primes in 100K For 100K, the correction constant was [- [log 100000. / 100000. 9592. ] or 1.087571. Paste statement on console, set prime_count [ llength [primesLowerThan 1000000 ] results in 78498 primes. For 1000K, the correction constant was [- [log 1000000. [/ 1000000. 78498. ] or 1.076332. Using the formula and above testcases for the modified_legendre_prime_constant, a one liner program can be developed. There is a possible warning for lengthy time calls on primesLowerThan for high numbers greater than 10K.
# scratch development on one liner program
# preceding from fixed or hard wired formula to general formula
proc tester1 nn { [- [log 10000. ] [/ 10000. 1229. ]] }
proc tester2 nn { [- [log $nn ] [/ [* $nn 1.] [ llength [ primesLowerThan $nn ]] ]] }
proc modified_legendre_prime_constant1 nn { [- [log $nn ] [/ [* $nn 1.] [ llength [ primesLowerThan $nn ]]]]}
# proc seemed to work better on the local TCL 8.6 set with a return statement?
proc modified_legendre_prime_constant2 nn { return [- [log $nn ] [/ [* $nn 1.] [ llength [ primesLowerThan $nn ]]]]}
# possible warning for lengthy time calls on primesLowerThan for high numbers greater than 10K
# need to keep isolating spaces in math ops statements
#Usage for 10K, modified_legendre_prime_constant 10000 returns 1.073643
#Usage for 100K, modified_legendre_prime_constant 100000 returns 1.087571
#Usage for 1000K, modified_legendre_prime_constant 1000000 returns 1.076332Subject: consider prime numbers as fish in a vast sea, TCL programming
As a mental exercise, lets consider prime numbers as fish in a vast sea of numbers, starting from the shoreline as the origin or zero. In this vast sea of fish, there are whole numbers and decimal numbers. The prime fish are whole numbers, but there are many other fish that are factorable or not defined as prime. The prime fish seem to be more common near the shoreline or origin, but the prime fish are rare or uncommon in some sections of the sea, especially as one goes further from the shoreline origin.
One can use the new TCL tools as nets to measure or sample the rarity of prime fish. Using the modified Legendre function, we can write a simple procedure or subroutine to sample the sea of numbers at intervals ( usually 100 units in the refs). Rounding numbers from the modified Legendre subroutine, we find that there are about 19 prime fish from 100. to 200., but only 7 prime fish from 1000000. to 1000100. Prime fish are becoming more rare as we travel away from the shoreline origin.
Considering the whole numbers only, and if we caught 19 prime fish from the 100. to 200., then the remaining fish in the net as whole numbers must be non primes, as expr((200.-100.-19. ) or 81. Remember that the modified Legendre function is not exact, but an decimal approximation for easy use and quick computer time in TCL. With a few lines of code, we can estimate the numbers of prime fish and factorable (non-prime) fish over the vast extent of the sea of number.
While the modified Legendre function is not exact, can we find sections of the sea where there are no prime fish or very low estimates of prime fish? Meaning, where there are few or no prime fish within the mesh size, granularity, and reach of our net calculations. The subroutine evaluation as delta leg 1000000000000 1000000000100 gives 3.64, suggesting 3 or 4 prime fish at 1E12. Some other more exact and time costly subroutines on the wiki reported 4.1 percent primes at 1E12 and 3 percent primes at 1E15, roughly 3 prime fish.
One Liner programs on Primes, Twin Primes, and Primes separated by Even Numbers
Here is the one liner program approach for various prime functions and approximations, although dependent on helper procs, math ops, and TCLLIB isprime proc. This section is not a replacement for the current TCL core and TCCLIB with much improvement since TCL4 and other <faster> language constructs. See better routines and current methods for primes in the TCL core distribution and TCLLIB. There are pros and cons to the one liner programs. Working with recursion, primes, and timing the procedures will quickly show the warts on the one liner programs. To gain speed and shorter computation times, one will generally have to access the TCL core distribution and TCLLIB. Functions math::numtheory::isprime, math::numtheory::firstNprimes, and math::numtheory::primesLowerThan are available in the TCCLIB math library. See TCLLIB & Tcllib Contents & math::numtheory Category Numerical Analysis.
In an 1849 letter, Gauss described his own results and the results of Legendre in evaluating the numbers of primes over some vast regions of the number line. The math in this section was worked out long ago by Gauss and Legendre. The modern terms and definitions here on prime number theory are more in historical interest to derive these simple TCL routines from the original work. Gauss postulated that the number of primes was <N> over < ln N>, using log for natural log hereafter. The gaussian_prime_density_approx is < number of primes > over < set of natural numbers from zero to upper limit>, <N/logN>/<N> , / $n [log $n ] / $n, which reduces to proc gaussian_prime_density_approx {aa} {/ 1. [log $aa]}. Another thought of Gauss would be to treat these prime ratios as probability. The probability of choosing a prime number from set of natural numbers from zero to upper limit would be equivalent to the gaussian prime density. The understanding here is the average gap between primes would be <N> over <N/log N> , $n / < [/ $n [log $n ]> , which reduces to gaussian_prime_average_gap_approx {aa} { log $aa}.
Legendre employed a corrective factor A of either 1 or approximately 1.08366 in his formula, P= N1 / (log (N1)-A). Commenting on the work of Legendre, Gauss pointed out that the corrective factor A must be a changing variable and appeared to decrease as N approached infinity. So the correcting factor A really seemed to be a changing function, not a constant. From Legendre, the number of primes was defined as P = <N>/ (< ln N>-A), 1/P = ( < ln N>-A)/<N>, ( < ln N>-A)=<N>*(1/P), A=( < ln N>-<N>*(1/P). Using the TCLLIB prime functions, the number of primes can be found from llength [ primesLowerThan $nn ]. So A as a constant or rather the function A evaluated near any given number would be the TCL expression { [- [log $nn / [* $nn 1. llength [ primesLowerThan $nn ] ] }. Continuing, the full procedure would be proc modified_legendre_prime_constant nn { [- [log $nn / [* $nn 1. llength [ primesLowerThan $nn]]}. Under the Legendre extension, the legendre_prime_density_approx is < number of primes > over < set of natural numbers from zero to upper limit>, <<N>/ (< ln N>-A>)/ <N>, <1>/ (< ln N>-A>). Continuing, the legendre_prime_density function might be proc legendre_prime_density_approx {nn} {/ 1. [- [log $nn 1.0866 ] }. The legendre_prime_gap_average might be proc legendre_prime_gap_average nn { [- [log $nn $A ] }, where $A approximates 1 or 1.0866.
Summary
Summary. In an 1849 letter, Gauss discussed findings on the number of primes in various regions of the number line. The historical background of this prime number theory is of interest today in developing simple TCL routines.
# average gap approximate between primes in near field,
# from Gauss in 1792/3 CE. approximate only, not exact
proc gaussian_prime_density_approx {aa} {[/ 1. [log $aa]]}
proc gaussian_prime_average_gap_approx {aa} { [log $aa]}
proc pg {aa} { [log $aa]}
# check from prime number series 3,5,7, near 5
# [- 5 3] =2 , [- 7 5] =2 , pg 5 > 1.6
# check from prime number series 23, 29, 31, 37, near 30
# [- 29 23]=6, [- 31 29]=2,.[- 37 31]= 6
# pg 30 = 3.401, (6+2+6)/3= 4.666
# list_twin_primes proc under test, list_twin_primes
# and isprime procs are recursion limited, using TCLLIB isprime here
proc list_twin_primes { aa bb cc} { for {set i $aa} {$i<=$bb} {incr i 1} { if {[isprime $i] && [isprime [+ $i $cc ] ] } { lappend boo $i [+ $i $cc ] } } ; return $boo}
# aa is lower limit or start number,
# bb is upper limit or end number.
# cc is separator number, usually even 2
# contains redundant commands for testing
puts "[list_twin_primes 3 25 2 ]"
puts "[list_twin_primes 3 25 4 ]"
puts "[list_twin_primes 3 25 6 ]"
puts "[list_twin_primes 3 25 10 ]"
# The original Dickson conjecture has separator even numbers 2,4,6 ... ?
# list_twin_primes 0 25 2 returns 3 5 5 7 11 13 17 19
# The sets <13 15> and <15 17> are separated by a even 2,
# but left out of answer.
# Note the 15 is not a prime number and has factors <3 5>.
# The set <13 17> has two primes, but separated by an even 4.
# reference On-Line Encyclopedia of Integer Sequences website
# OEIS A077800 discussed that the twin prime sets <p,p+2> are
# (3, 5), (5, 7), (11, 13), (17, 19),
# (29, 31), (41, 43), (59, 61), (71, 73),
# (101, 103), (107, 109), (137, 139)...
# OEIS A275021 has samples of <p,p+4> and omits pairs of <p,p+2>
# 79, 83, 127, 131, 163, 167, 379, 383, 397, 401, 439, 443,...
# list_twin_primes 75 135 4 returns 79 83 103 107 127 131
# OEIS A023201 has some samples of <p,p+6>
# 5, 7, 11, 13, 17, 23, 31, 37,
# 41, 47, 53, 61, 67, 73, 83, 97, 101
# list_twin_primes 3 25 6
# returns 5 11 7 13 11 17 13 19 17 23 23 29
# list_twin_primes 3 25 10
# returns 3 13 7 17 13 23 19 29Table Results on Twin Primes for 2,4,6,10 Separators
| table | Twin Primes for 2,4,6,10 Separators | printed in | TCL format | |
|---|---|---|---|---|
| result | lower limit | upper limit | separator integer | comment, if any |
| elements in list | lower limit | upper limit | separator integer | comment, if any |
| 3 5 5 7 11 13 17 19 | 3 | 25 | 2 | |
| 3 7 7 11 13 17 19 23 | 3 | 25 | 4 | |
| 5 11 7 13 11 17 13 19 17 23 23 29 | 3 | 25 | 6 | |
| 3 13 7 17 13 23 19 29 | 3 | 25 | 10 |
2021 Newsflash, TCLLIB has twin primes and cousin primes routines in TCLLIB:math ticket pipeline
gold 5/13/2021.
closer: arjenmarkus AM
Emailed icomment from AM: I used the sample code to create two new procedures:
listPrimePairs listPrimeProgressions
The first proc listPrimePairs returns a list of pairs of primes that differ by a given number and the second proc listPrimeProgressions returns a list of arithmetic progressions of primes that differ by the given number.
Prime Difference Function
The Prime Difference Function is the set of Prime gaps, which are the differences between the consecutive primes listed in the prime counting function < TCLLIB primesLowerThan> . Successive differentiating of the Prime Counting Function is possible.
scratch code under test.
# pseudocode
set ncat [ llength [primesLowerThan 20]]
# 8
set dd [ primesLowerThan 20 ]
# 2 3 5 7 11 13 17 19 ;# oeis 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
set dd { 2 3 5 7 11 13 17 19 }
proc list_twin_primes { aa bb cc} { for {set i $aa} {$i<=$bb} {incr i 1} { if {[isprime $i] && [isprime [+ $i $cc ] ] } { lappend boo $i [+ $i $cc ] } } ; return $boo}
# aa is lower limit or start number,
# bb is upper limit or end number.
# cc is separator number, usually even 2
# under test, contains redundant commands for testing
proc pdf { aa bb cc} { foreach {a b} [ primesLowerThan 20 ] { lappend booo [- $b $a ] } ; return $booo }
pdf 0 20 2
# 1 2 2 2
proc pdf2 { nn} { foreach {a b} [ primesLowerThan $nn ] { lappend boo [- $b $a ] } ; return $boo }
pdf2 20
# subtracting alternate pairs? <2 3> <5 7> <11 13> <17 19>
proc pdf3 { nn} { foreach {a b} [ primesLowerThan $nn ] { lappend boo [- $b $a ] } ; return $boo }
pdf2 20
# 1 2 2 2
# messing up here, OEIS A001223 has Prime gaps: differences between consecutive primes.
# 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4,
set lister {90.5 47 58 29 22 32 55 5 55 73.5}
set i 1
[ lindex $a $i ] ;# 47
[ lindex $a [+ $i 1 ] ] ;# 58
[- [ lindex $a [+ $i 1 ] ] [ lindex $a $i ] ] ;# 11
# set r [ lister[i + 1] - lister[i] for i in range(len(lister)-1)]
Table: Prime Difference Function
| table | printed in | TCL format |
|---|---|---|
| line number | prime function series | comment, if any |
| 0 | 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 | primes output from TCLLIB primesLowerThan |
| 1 | 1 2 2 4 2 4 2 4 6 2 6 4 2 4 | gaps & prime difference function 1’ |
| 2 | 1 0 2 -2 2 -2 2 2 -4 4 -2 -2 2 | prime difference function 2’,note that some pairs have form < -X X >, < X -X >, |
| 3 | -1 2 -4 4 -4 4 0 -6 8 -6 0 4 | difference function 3’ |
| 4 | 3 -6 8 -8 8 -4 -6 14 -14 6 4 | difference function 4’ |
| 5 | -9 14 -16 16 -12 -2 20 -28 20 -2 | difference function 5’ |
| 6 | 23 -30 32 -28 10 22 -48 48 -22 | difference function 6’ |
| 7 | -53 62 -60 38 12 -70 96 -70 | difference function 7’ |
| 8 | 115 -122 98 -26 -82 166 -166 | difference function 8’ |
| 9 | -237 220 -124 -56 248 -332 | difference function 9’ |
| 10 | 457 -344 68 304 -580 | difference function 10’ |
Table: Rarity of Primes as percent reported from Modified_Legendre_primes function
| table Rarity of Primes | mod_percent {n} | Modified Legendre P. Function | Prime Counting Function | printed in | tcl wiki format | |
|---|---|---|---|---|---|---|
| testcase | power or order | TCL proc percent from mod legendre_primes | mod legendre_primes | prime_pi | percent prime_pi | comment if any |
| testcase 1 | .5E1 | not acc. | 9.5097 not acc. | 3 | 60.0 | expr (3./5.)*100. |
| testcase 2 | 1E1 | not acc. | 8.2039 not acc. | 4 | 40. | expr (4./10.)*100. |
| testcase 3 | 1E2 | 28.397 | 28.397 | 25 | 25. | expr (25./1E2)*100. |
| testcase 4 | 1E3 | 17.17 | 171.7 | 168 | 16.8 | expr (168./1E3)*100. |
| testcase 5 | 1E4 | 12.3051 | 1230.514 | 1229 | 12.29 | expr (1229./1E4)*100. |
| testcase 6 | 1E5 | 9.5884 | 9588.402 | 9592 | 9.592 | expr (9592./1E5)*100. |
| testcase 7 | 1E6 | 7.854 | 78543.178 | 78498 | 7.8498 | f(x) =(( prime_pi (x))/x)*100. |
| testcase 8 | 1E7 | 6.651 | 665139.699 | 664579 | 6.64579 | |
| testcase 9 | 1E8 | 5.768 | 5768003.712 | 5761455 | 5.761455 | |
| testcase 10 | 1E9 | 5.092 | 50917518.829 | 50847534 | 5.0847534 | |
| testcase 11 | 1E10 | 4.557 | 455743003.601 | 455052511 | 4.55052511 | |
| testcase 12 | 1E11 | 4.125 | 4124599868.665 | 4118054813 | 4.118054813 | |
| testcase 13 | 1E12 | 3.767 | 37668527415.329 | 37607912018 | 3.7607912018 | |
| testcase 11 | 1E13 | 3.466 | 346621096884.653 | 346065536839 | 3.46065536839 | |
| testcase 12 | 1E14 | 3.21 | 3210012022164.23 | 3204941750802 | 3.204941750802 | |
| testcase 13 | 1E15 | 2.989 | 29890794226981.8 | 29844570422669 | 2.9844570422669 |
Testcases Section
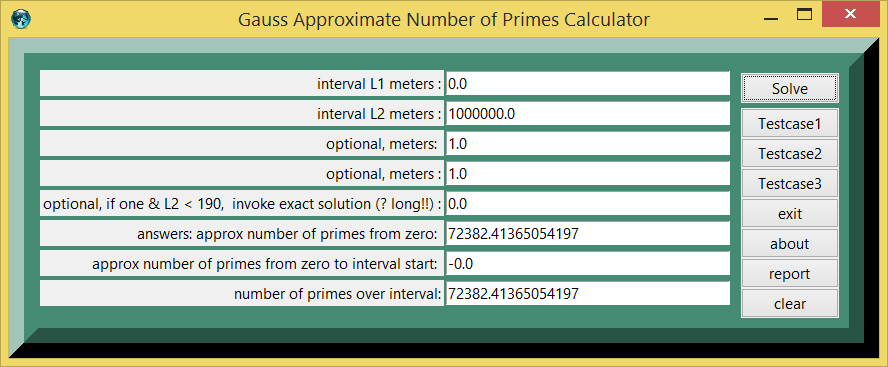
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 1 | |
| 0.0 : | interval L1 meters | |
| 1000000.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 72382.41365054197 : | answers:approx_number_primes | |
| -0.0 : | approx_number_primes_interval_start | |
| 72382.41365054197 : | approx. number_primes_over_interval | |
| 78498: | exact solution from internet | |
| 8.4 : | error percent |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 2 | |
| 0.0 : | interval L1 meters | |
| 5.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 3.1066746727980594 : | answers:approx_number_primes | |
| -0.0 : | approx_number_primes_interval_start | |
| 3.1066746727980594 : | number_primes_over_interval | |
| 3.0 : | exact solution number_primes_over_interval | |
| 2.0 3.0 5.0 : | list number_primes_over_interval of 0 to 5 | |
| 0.55 : | error percent |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 3 | |
| 0.0 : | interval L1 meters | |
| 10.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 4.3429448190325175 : | answers:approx_number_primes meters | |
| -0.0 : | approx_number_primes_interval_start | |
| 4.3429448190325175 : | number_primes_over_interval | |
| 4.0 : | exact solution number_primes_over_interval | |
| 2.0 3.0 5.0 7.0 : | list number_primes_over_interval of 0 to 10 | |
| 8.5 : | error percent |
Testcase 4
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 4 | |
| 0.0 : | interval L1 meters | |
| 100.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 1.0 : | optional,if one, invoke exact solution (? long) | |
| 21.71472409516259 : | answers:approx_number_primes meters | |
| -0.0 : | approx_number_primes_interval_start | |
| 25 : | exact solution number_primes_over_interval | |
| 2.0 3.0 5.0 7.0 11.0 13.0 17.0 19.0 23.0 29.0 31.0 37.0 41.0 43.0 47.0 53.0 59.0 61.0 67.0 71.0 73.0 79.0 83.0 89.0 97.0 : | list number_primes_over_interval | |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | exact solution from internet | |
| 5.6 : | error percent |
Testcase 5
| table 5 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 5 | |
| 0.0 : | interval L1 meters | |
| 190.0 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 1.0 : | optional,if one, invoke exact solution (? long) | |
| 36.2110021579845 : | answers:approx_number_primes meters | |
| -0.0 : | approx_number_primes_interval_start | |
| 42 : | exact number_primes_over_interval meters | |
| 2.0 3.0 5.0 7.0 11.0 13.0 17.0 19.0 23.0 29.0 31.0 37.0 41.0 43.0 47.0 53.0 59.0 61.0 67.0 71.0 73.0 79.0 83.0 89.0 97.0 101.0 103.0 107.0 109.0 113.0 127.0 131.0 137.0 139.0 149.0 151.0 157.0 163.0 167.0 173.0 179.0 181.0 : | list number_primes_over_interval | |
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181 | exact solution from internet | |
| 15.9 : | error percent |
Testcase 6
| table 6 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 2 | |
| 0.0 : | interval L1 meters | |
| 1e+27 : | meters L2 meters | |
| 1.0 : | meters | |
| 1.0 : | meters | |
| 0.0 : | optional,if one, invoke exact solution (? long) | |
| 1.608498081123155e+25 : | answers:approx_number_primes | |
| -0.0 : | approx_number_primes_interval_start | |
| 1.608498081123155e+25 : | approx. number_primes_over_interval from 0 to 10E26 | |
| 1,699,246,750,872,437,141,327,603 28,883,358,936,853,188,823,261 155,891,678,121 58.850: | exact solution from internet | |
| 5.6 : | error percent |
Testcase 7 , devil's notch
| table 7 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number: | 7 | |
| 550.0 : | interval L1 | devil's notch |
| 650.0 : | end number L2 | |
| 1.0 : | optional,if one, invoke exact solution (? long) | |
| 100.35553088418682 : | answers: gauss function ~number_primes | |
| 120.51962806243556 : | legendre function ~number_primes | |
| 100.35553088418682 : | gauss approx_number_primes | |
| 87.164361842509408 : | gauss approx_number_primes_interval_start | |
| 118 : | gauss number_primes_over_interval | |
| 120.51962806243556 : | legendre_function number_primes_N1 | |
| lister {557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647}: | exact solution from prime_counting_functionx | |
| 17 : | prime_counting_function over interval |
Screenshots Section
figure 1.
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
figure 10.
figure 11.
figure 12.
References:
- Primes
- Oneliner's Pie in the Sky
- One Liners
- Comparing Tcl and Python
- Primes Sieve - on a resizable canvas from uniquename
- TCLLIB ::math::numtheory
- https://en.wikipedia.org/wiki/Prime-counting_function
- http://sweet.ua.pt/tos/primes.html#i
- http://mathworld.wolfram.com/PrimeCountingFunction.html
- http://www.math.uni-bonn.de/people/jbuethe/topics/AnalyticPiX.html
- http://primes.utm.edu/notes/rh.html
- http://numbers.computation.free.fr/Constants/Primes/pixtable.html
- http://numbers.computation.free.fr/Constants/constants.html
- on line prime number generator, see
- http://www.miniwebtool.com/list-of-prime-numbers/?to=50
- Mathematician pair find prime numbers aren't as random as thought, March 15, 2016 by Bob Yirka,
- ref Robert Lemke Oliver and Kannan Soundararajan, Stanford University
- google < Prime number theorem Wikipedia >
- Probability that a number is prime, John D. Cook, 6 October 2010
- Probability of Next Prime Digit, Kevin's Math Page, Kevin Gong,March 17th, 2016
- Mathematicians Discover Prime Conspiracy, Erica Klarreich , March 13, 2016, Quanta Magazine
- Prime Probability: Catch the Wave, Michael M. Ross , Excel spreadsheet, Jan2008
- Prime Numbers and Their Statistical Properties,Dr. Phillip M. Feldman
- 19TH CENTURY MATHEMATICS - GAUSS, The Story of Mathematics
- A Conjecture about the Density of Prime Numbers,
- Lincoln Almir AMARANTE RIBEIRO, Departamento de Física,
- Universidade Federal de Minas Gerais, good explanation
- Dan Rockmore Stalking the Riemann Hypothesis, The Quest to Find the Hidden Law of Prime Numbers
- J. Pintz. On Legendre's prime number formula. Amer. Math. Monthly 87 (1980)
- Dusart, Pierre. Estimates of some functions over primes without r.h
- Ref. proc sum_primes_to by dkf
- from Comparing Tcl and Python on TCL WIKI
- Ref. Sieve of Eratosthenes « Python recipes « = code.activestate.com/recipes/117119/
- Karskens, Michiel, On the Theory of Numbers: A Simple Explanation of
- the Sequence of Prime Numbers, December 2017
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Gauss approximate number of primes calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 15may2016
# comment follows from gold, 12Dec2018
# pretty print from autoindent and ased editor
# Gauss Approximate Number of Primes Calculator V2
# written on Windows XP on TCL
# working under TCL version 8.6
# Revamping older program from 2016.
package require Tk
package require math::numtheory
#namespace path {math::numtheory}
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {interval number L1 :} }
lappend names {end number L2 :}
lappend names {optional, if one & L2 < 190, invoke exact solution (? long!!): }
lappend names {answers: gauss function ~number_primes for N1 :}
lappend names {legendre function ~number_primes for N1 :}
lappend names {gauss approx number of primes from zero: }
lappend names {gauss approx number of primes from zero to interval start: }
lappend names {gauss number of primes over interval:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Gauss Approximate Number of Primes V2
from TCL ,
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "About" -message $msg }
# ref. TCLLIB::math::numtheory::prime_counting_functionx
# ref. alternate TCLLIB::math::numtheory::isprime
proc self_help {} {
set msg " Gauss Approximate Number of Primes V2
from TCL Club ,
# self help listing
# problem, Gauss Approximate Number of Primes V2
# 3 givens follow.
1) interval number L1:
2) end number L2:
3) optional, if one & L2 < 190, invoke exact solution (? long!!):
# Recommended procedure is push testcase
# and fill frame,
# change first three entries etc, push solve,
# and then push report.
# Report allows copy and paste
# from console to conventional texteditor.
# For testcases, testcase number is internal
# to the calculator and will not be printed
# until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas
or formulas grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 12Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc prime_counting_function { start end } {
set start [int $start ]
set end [int $end ]
set counter 0
if { $start > 1 } { set counter $start }
set end $end
set prime_counting_function 0
while { $counter < $end } {
incr counter
incr prime_counting_function [isprime $counter ]
}
return $prime_counting_function }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global switch_factor big_giant_list legendre_function
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set L1 $side1
set L2 $side2
set N1 $side2
set switch_factor $side3
set approx_number_primes [/ $N1 [log $N1 ] ]
set legendre_function [/ $N1 [- [log $N1 ] 1.08366 ] ]
# conditions, all numbers real and positive.
# conditions L1 =! 1 and L2 > L1, otherwise division by zero and undefined Q's.
# if { $L1 == 1.0 } { set $L1 0.0 }
set approx_number_primes_interval_start [/ $L1 [log $L1 ] ]
set approx_number_primes_over_interval [- [/ $L2 [log $L2 ] ] [/ $L1 [log $L1 ] ] ]
set side4 $approx_number_primes
set side5 $legendre_function
set side6 $approx_number_primes
set side7 $approx_number_primes_interval_start
set side8 $approx_number_primes_over_interval
if { $switch_factor > 0 && $L2 < 200 } { exact_solution }
}
proc listprimes { aa bb} {lappend booboo 2.0; for {set i 1} {$i<=$bb} {incr i 2} { if {[isprime $i] } {lappend booboo [expr 1.*$i] } };return $booboo}
#returns list of prime numbers from aa to bb, usage [listprimes 0 25],
# answer is 2.0 3.0 5.0 7.0 11.0 13.0 17.0 19.0 23.0,
# list returned as real numbers, not counting 1.0 unity
proc exact_solution {} {
global side1 side2 side3 side4 side5
global side6 side7 side8 big_giant_list prime_counting
set big_giant_list [ listprimes $side1 $side2 ]
set side8 [ llength $big_giant_list ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global switch_factor big_giant_list legendre_function
global testcase_number
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Gauss Approximate Number of Primes V2 Report, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number:|$testcase_number | |&"
puts "&| $side1 :|interval L1 | |&"
puts "&| $side2 :|end number L2 | |& "
puts "&| $side3 :|optional,if one, invoke exact solution (? long) | |& "
puts "&| $side4 :|answers: gauss function ~number_primes| |&"
puts "&| $side5 :|legendre function ~number_primes| |&"
puts "&| $side6 :|gauss approx_number_primes | |&"
puts "&| $side7 :|gauss approx_number_primes_interval_start | |&"
puts "&| $side8 :|gauss number_primes_over_interval | |&"
puts "&| $legendre_function :|legendre_function number_primes_N1| |&"
if {$switch_factor > 0.0} { puts "&| [prime_counting_function $side1 $side2 ] :|prime_counting_function over interval| |&" }
if {$switch_factor > 0.0 && $side2 < 190.} {puts "&| $big_giant_list :|list number_primes_over_interval | |&" }
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 0.0 1E1 1.0 4.3 8.20 4.3 0.00 4.30}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 0.0 5.0 1.0 3.1 9.50 3.1 0.00 3.10 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1E3 1E6 1.0 7E5 7E5 72382.0 0.0 72382.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Gauss Approximate Number of Primes Calculator V2"Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program used to build csv spreadsheet charts.
# autoindent from ased editor
# console program for graph numbers
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# TCL WIKI , 12dec2016
console show
package require math::numtheory
#namespace path {math::numtheory}
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc factors {} {
set counter 0
set prime_counting_function 0
while {$counter < 500} {
puts " [* $counter 1.] , [/ [* $counter 1.] [log [* $counter 1.]] ], [isprime $counter ], $prime_counting_function "
incr counter
incr prime_counting_function [isprime $counter ]
}
return }
factorsconsole output
2.0 , 2.8853900817779268, 1, 1 3.0 , 2.7307176798805122, 1, 2 4.0 , 2.8853900817779268, 0, 2 5.0 , 3.1066746727980594, 1, 3 6.0 , 3.3486637593074837, 0, 3 7.0 , 3.5972883965882549, 1, 4 8.0 , 3.8471867757039027, 0, 4 9.0 , 4.0960765198207678, 0, 4 10.0 , 4.3429448190325175, 0, 4
# under test, biasing approx. from interval to save computer time
proc prime_counting_function { start end } {
set counter 0
if { $start > 1 } { set counter [int $start ] }
set end [int $end ]
set prime_counting_function 0
while { $counter < $end } {
incr counter
incr prime_counting_function [isprime $counter ]
}
return $prime_counting_function }
proc biased_count { N1 } {
set N1 [int $N1 ]
set bias1 [* 1. [ prime_counting_function [int [* $N1 .99] ] $N1 ]]
set bias2 [* 1. [ prime_counting_function $N1 [int [* $N1 1.01]] ]]
puts " $bias1 "
puts " $bias2 "
set bias 1.
set approx_number_primes 1.
set bias [expr $bias2/ double($bias1) ]
puts " $bias $bias2 $bias1 "
set approx_number_primes [* [/ $N1 [log $N1 ] ] $bias ]
return $approx_number_primes
}Console program for devil's notch
# pretty print from autoindent and ased editor
# testing devil's notch
# prime number function from TCLLIB
# written on Windows XP
# working under TCL version 8.6.6
# gold on TCL WIKI , 20dec2017
package require Tk
package require math::numtheory
package require math::constants
#package require math::bigfloat
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::constants }
console show
# corrected legendre_function
proc leg {N1 N2 } {
set legendre_function [/ $N1 [- [ ::tcl::mathfunc::log $N1 ] 1.08366 ] ]
set legendre_functionx [/ $N2 [- [ ::tcl::mathfunc::log $N2 ] 1.08366 ] ]
return [- $legendre_functionx $legendre_function ]
}
set numberx [ ::math::numtheory::prime_counting_functionx 450 550 ]
puts "prime counting function $numberx corrected legendre [ leg 450. 550. ] "
set numberx [ ::math::numtheory::prime_counting_functionx 550 650 ]
puts "prime counting function $numberx corrected legendre [ leg 550. 650. ] "
set numberx [ ::math::numtheory::prime_counting_functionx 650 750 ]
puts "prime counting function $numberx corrected legendre [ leg 650. 750. ] "
# padded statements into <local> ::math::numtheory::prime_counting_functionx
# for list of primes in interval
#if {[::math::numtheory::isprime $counter ] } { lappend lister $counter }
# }
# puts $listerAlternate Console programs for prime_counting_function
# pretty print from autoindent and ased editor
# console program for prime_counting_function
# keywords prime counting function
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL WIKI, 4feb2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
console show
# adapted from sum_primes_to by dkf
# from Comparing Tcl and Python on TCL WIKI
# advantage: no dependency on expr or isprime.
# large numbers > 10E3 can take a long time.
proc prime_counting_function {n {i 1}} {
set total 0
incr n 0
for {set q [+ $i $i ]} {$q < $n} {incr q} {
if {![info exists d($q)]} {
incr total
lappend d([* $q $q ]) $q
} else {
foreach p $d($q) {
lappend d([+ $p $q ]) $p
}
unset -nocomplain d($q)
}
}
return $total
}
puts " prime_counting_function for 100 , answer [prime_counting_function 100]
puts " time note [ time {prime_counting_function 100} 100 ] "
# prime_counting_function for 100 , answer 25
# time note 273.35 microseconds per iteration # pretty print from autoindent and ased editor
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL WIKI , 2feb2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory}
set tclprecision 17
console show
# based on all_primes proc in Sample Math Programs on TCL WIKI
proc prime_counting_functiont {max} {
# from rwt? on TCL WIKI
set counter 1
set primes [list 2]
for {set test 3} {$test <= $max} {incr test 2} {
set maxTest [int [sqrt $test ]]
foreach prime $primes {
if {$prime > $maxTest} {
# puts $test list omitted for time save
lappend primes $test
incr counter
break
}
if {![% $test $prime ]} {
break
}
}
}
return $counter
}
puts " prime_counting_functiont answer [ prime_counting_functiont 100]"
puts " prime_counting_functiont time note [ time { prime_counting_functiont 100 } 300 ] "
# prime_counting_functiont answer 25
# prime_counting_functiont time note 165.896 microseconds per iteration | table | timing on prime testers from TCL WIKI and “homebrew” | printed in | tcl wiki format |
|---|---|---|---|
| program | principle authors | time microseconds | comment, if any |
| ispprime | off_site caveat | 1.75 | testing n=100 for all, divisor algorithm,n<? |
| ::numtheory::isprime | TCLLIB | 2.623 | testing n=100 for all |
| prime: | RS | 3.313 | testing n=100 for all |
| primeCheckFermat : | rwm | 7.12 | working fast, but checks all cases? |
| primetest : | WIKI? | 21.443 | |
| primetest2 : | RS | 21.853 | |
| isprimex : | perl_hacker | 29.973 | |
| prime_counting_functiont : | modified all_primes from rwt? on TCL WIKI | 159.25 | Px (100)=25 |
| prime_counting_function plus math::isprime : | homebrew | 245.51 | Px (100)=25 |
| prime_counting_functionx minus math::isprime : | homebrew | 263.5 | Px (2 100)=25 |
Console program for sum of reciprocal squares of prime numbers.
The prime zeta function is a subset of the Riemann Zeta Function. Using powers of prime numbers in the denominator, a general TCL expression might be P(n)= 1./(** 2 n)+1./(** 3 n)+1./(** 5 n) ... with n as the positive power or order. P(1) is divergent.
P(2), where P is the "prime zeta function," at infinity is 0.4522474200. Testcase1 is expr { 1./(2*2)+1./(3*3)+1./(5*5)}, 0.4011111111111111.TCL proc gives answer 0.4011 , time note 27.809 microseconds per iteration. Testcase2 is expr { 1./(2*2)+1./(3*3)+1./(5*5)+1./(7*7)+1./(11*11)+1./(13*13)}], 0.4357008969496481. TCL proc gives answer 0.4357, time note 38.409 microseconds per iteration. Testcase3 for 10000 , proc gives answer 0.4522376, time note 48100.309 microseconds per iteration.
# following statements can be pasted into TCL console
set project 1.0
set P_2 expr { 1./(2*2)+1./(3*3)+1./(5*5)} #0.40111
set P_2 expr { 1./(2*2)+1./(3*3)+1./(5*5)+1./(7*7)+1./(11*11)+1./(13*13)} # 0.43570 Proc could be modified with args to return P(2),P(3) etc. P(1) is divergent. I don't see this in math::numtheory::isprime, but TCLLIB is a big file system. Also checking division by 2 would eliminate some steps.
Table for prime_zeta_function
| table testcases number | printed in | tcl wiki format | |||
|---|---|---|---|---|---|
| testcase | P(order) | TCL n value | TCL proc prime_zeta_function | P(order) standard at inf | comment, if any |
| testcase 1 | 2 | 1E6 | 0.45224735226537194 | 0.452247 | |
| testcase 2 | 3 | 1E6 | 0.17476263929927133 | 0.174763 | |
| testcase 3 | 4 | 1E6 | 0.076993139764243643 | 0.0769931 | |
| testcase 4 | 5 | 1E6 | 0.035755017483924012 | 0.035755 | |
| testcase 5 | 6 | 1E6 | 0.017070086850636487 | 0.0170701 | |
| testcase 6 | 7 | 1E6 | 0.0082838328561335856 | 0.00828383 | |
| testcase 7 | 8 | 1E6 | 0.0040614053665178288 | 0.00406141 |
---
# pretty print from autoindent and ased editor
# console program for prime_zeta_function
# keywords sum squares prime zeta function Sieve Eratosthenes
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL WIKI, 4feb2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
console show
# adapted from sum_primes_to by dkf
# from Comparing Tcl and Python on TCL WIKI
# advantage: no dependency on expr or isprime.
# large numbers n > 10E3 can take a long time.
# P(order 1) is divergent, P(n),n>1 should be convergent.
proc prime_zeta_function {bb n} {
# tally sequence of prime numbers via the Sieve of Eratosthenes.
# n is highest integer to test
# i subintegers to test as factors
# D() # map composite integers to primes witnessing their compositeness
# q = integer to test for primality (usually starts at 2 )
# total here, sum of reciprocals of prime squares or powers
# bb is square or power for reciprocal denominator
# prime zeta function P(1) is divergent at inf, higher P() converge
# if q and p are odd, q+2*p will always be odd.
# all even numbers n() are not prime, except 2.
set total 0
incr n 0
set i 1
for {set q [+ $i $i ]} {$q < $n} {incr q} {
if {![info exists d($q)]} {
# add 1/n**bb to tatal if n prime
set total [+ $total [/ 1. [* $q $q ] ]]
# add to current map
lappend d([* $q $q ]) $q
} else {
# move each witness to its next multiple
foreach p $d($q) {
lappend d([+ $p $q ]) $p
}
unset -nocomplain d($q)
# dump map
}
}
return $total
}
puts " prime_zeta_function for {2 6} , answer [prime_zeta_function 2 6] "
puts " time note [ time {prime_zeta_function 2 5} 100 ] "
puts " prime_zeta_function for {2 10000} , answer [prime_zeta_function 2 10000 ] "
puts " time note [ time {prime_zeta_function 2 10000} 100 ] "
# prime_zeta_function for {2 6} , answer 0.40111111111111108
# time note 11.390000000000001 microseconds per iteration
# prime_zeta_function for {2 10000} , answer 0.45223760433995064
# time note 71381.509999999995 microseconds per iteration proc report {n} {
set count 1
set lister {}
set lister {0. 0.452247 0.174763 0.0769931 0.035755 0.0170701 0.00828383 0.00406141 0.00200447 0.000993604 }
puts "%|table testcases number||||printed in| tcl wiki format|% "
puts "%|testcase |P(order)|TCL n value |TCL proc prime_zeta_function |P() standard at inf | comment, if any|% "
foreach item { 2 3 4 5 6 7 8 } {
puts "&| testcase $count | $item |1E6 |[ prime_zeta_function $item 1000000 ] | [lindex $lister $count]||&"
incr count 1
}}
report 2References:
- Primes
- Oneliner's Pie in the Sky
- One Liners
- Comparing Tcl and Python
- TCLLIB ::math::numtheory
- en.wikipedia.org/wiki/Prime-counting_function
- sweet.ua.pt/tos/primes.html
- mathworld.wolfram.com/PrimeCountingFunction.html
- Prime zeta function, Wikipedia
- Prime Zeta Function, from Wolfram MathWorld
- Riemann zeta function, Wikipedia
- Sample Math Programs on TCL WIKI
- On the Number of Prime Numbers less than
- a Given Quantity,Bernhard Riemann,November 1859.
Credits on One Liner Programs
- WIKI BOOKS, Tcl_Programming_Introduction
- license https://creativecommons.org/licenses/by-sa/3.0/legalcode
- creativecommons.org/licenses/by-sa/3.0/
- en.wikibooks.org/wiki/Tcl_Programming_Introduction >>>pdf<<<
- Sample Math Programs, item 2, RS
- TCLLIB math::mean is quicker by a third over some homebrew code.
- Additional math functions
- en.wikipedia.org One-liner_program
- One liners of Basic and history, 10_PRINT_121114.pdf
- Summing a list
- Tcllib Contents
- stackoverflow.com/questions 36832927 using-globs-in-perl-replace-one-liner-in-tcl-script
- www.rexegg.com regex-perl-one-liners
- Regular Expressions Cookbook, Second Edition
- Learning Regular Expressions
- Beyond Regular Regular Expressions
- Mastering Regular Expressions, 3e
- # credit Tcl and Tk Programming for the Absolute Beginner by KURT WALL
- bbcmicro.co.uk on Commodore Basic
- Acorn User One-Line Games (Escape From Voros, Lexxias, Race To Varpon,
- Storm Clouds Over Zaqqit, Zander (AKA Lurch))". bbcmicro.co.uk on Commodore Basic
- blog.eduonix.com, perl_programming,learn-one-liners-perl-programming
- en.wikipedia.org , One-liner_program
- RUN magazine issue 35 on Basic language
- Richard Socher, Perl Scripts And One Liners
- Introduction to Perl One-Liners (PDF), Peteris Krumins
- Perl one-liner if else logic - Stack Overflow
- How to Match Multiple Lines using Regex in Perl One-liners
- By Eric Ma , In Programming, Tutorial
- Time
- How to Measure Performance
- timers
^ [range]
- Category Performance
- see www.altparty.org archive/invi.tcl Setok ref.
- Why Tcl is so much slower than Perl, pros and cons
- Playing with recursion
- Category Numerical Analysis
- TCLLIB numtheory section
- Gauss Approximate Number of Primes and eTCL demo example calculator
- math::numtheory::isprime
- math::numtheory::firstNprimes
- math::numtheory::primesLowerThan
- math::numtheory::primeFactors
- math::numtheory::numberPrimesGauss
- math::numtheory::numberPrimesLegendre
- math::numtheory::numberPrimesLegendreModified
- math::numtheory::differenceNumberPrimesLegendreModified
- On-Line Encyclopedia of Integer Sequences , OEIS
- Andrew Granville, Primes in intervals of bounded length, Joint Math Meeting, Jan 17 2014.
- J. C. Evard, Twin primes and their applications, archived Pdf
- James Maynard, Small gaps between primes, arXiv:1311.4600 , 2013, Annals of Mathematics,
Comments Section
Please place any comments here, Thanks.
Draft on Pseudocode Format
# Pseudocode for the prime_counting_function program: 1. Define a procedure named prime_counting_function that takes two parameters: start and end. 2. Convert the start and end parameters to integers. 3. Initialize a counter variable to 0. 4. If the start parameter is greater than 1, set the counter variable to the value of the start parameter. 5. Set the end variable to the value of the end parameter. 6. Call the prime_counting_function procedure recursively with a counter of 0. 7. While the counter is less than the end value: a. Increment the counter by 1. b. Increment the prime_counting_function by the result of the isprime function called with the counter value.
Draft on Pseudocode format
The prime_counting_function is a recursive procedure that counts the number of prime numbers between the start and end values. The program initializes a counter variable to keep track of the current number being checked for primality. If the start value is greater than 1, the program sets the counter to the start value. The program then iterates through each number from the start to the end value, incrementing the counter and checking if each number is prime using the isprime function. The prime_counting_function recursively calls itself with an updated counter value until the counter reaches the end value. The function returns the total count of prime numbers found within the specified range.
an algorithm for a prime counting function that calculates the number of prime numbers between a start and end value.
1. Define a procedure named prime_counting_function that takes two parameters: start and end. The first step defines a procedure called prime_counting_function that takes two parameters, start and end. This procedure will be responsible for counting the number of prime numbers between the start and end values.
2. Convert the start and end parameters to integers. This step ensures that the start and end values are of the integer data type, which is necessary for counting prime numbers.
3. Initialize a counter variable to 0. The counter variable is initialized to 0 to keep track of the current number being checked for primality.
4. If the start parameter is greater than 1, set the counter variable to the value of the start parameter. This step checks if the start value is greater than 1. If it is, the counter variable is set to the start value, which means the counting will start from the start value.
5. Set the end variable to the value of the end parameter. This step sets the end variable to the end parameter, which will be used to determine when the counting should stop.
6. Call the prime_counting_function procedure recursively with a counter of 0. This step initiates the recursive process by calling the prime_counting_function procedure with a counter of 0. The recursive call will continue until the counter reaches the end value.
7. While the counter is less than the end value: a. Increment the counter by 1. b. Increment the prime_counting_function by the result of the isprime function called with the counter value. This part of the pseudocode describes the main loop of the prime counting function. The loop continues as long as the counter is less than the end value. Within the loop, the counter is incremented by 1, and the isprime function is called with the current counter value. The result of the isprime function is added to the prime_counting_function variable, which keeps track of the total count of prime numbers found within the specified range.Draft. A program that accurately counts the number of prime numbers between a given start and end value.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |
arjen - 2020-09-02 14:44:34
IF you check the Page on the Prime Number Theorem you will find a whopping large number, the (first) Skewes number in relation to the statement "pi(x) ~c Li(x)" ... It fascinates me that people can find out such things :).