The Q function
Richard Suchenwirth 2002-11-17 - In Douglas Hofstadter's book Goedel, Escher, Bach I found mention of "a little mystery in number theory", the heavily recursive Q function
Q(n) = Q(n - Q(n-1)) + Q(n - Q(n - 2)) if n>2 Q(1) = Q(2) = 1
which, though clearly defined (sort of Fibonacchi to the second power), produces a sequence of ever more puzzling numbers. Reason enough to start up a tclsh and try myself...
proc Q n {
if {$n<=2} {return 1}
expr {[Q [expr {$n - [Q [expr {$n - 1}]]}]]
+ [Q [expr {$n - [Q [expr {$n - 2}]]}]]}
}Whew, seven closing braces/brackets! More than Lisp would need parens! And this can be expected to run slow, due to the four recursions in every non-trivial call, so I very soon added a caching (memoizing) version, which remembers previous results and only does what's really needed, for comparing performance:
proc Q' n {
global Q
if {![info exists Q($n)]} {
if {$n<=2} {
set Q($n) 1
} else {
set Q($n) [expr {[Q' [expr {$n - [Q' [expr {$n - 1}]]}]]
+ [Q' [expr {$n - [Q' [expr {$n - 2}]]}]]}]
}
}
set Q($n)
}Both return the sample results in Hofstadter's book, so appear correct. Timing however is very different (even when duly clearing the cache before testing Q' - [Q 30] was already intolerably slow on my box at home):
% time {catch {unset Q};Q 10}
17624 microseconds per iteration
% time {catch {unset Q};Q' 10}
4873 microseconds per iteration
% time {catch {unset Q};Q 20}
2683731 microseconds per iteration
% time {catch {unset Q};Q' 20}
10278 microseconds per iteration
10 % time {catch {unset Q};Q 30}
337324223 microseconds per iteration
11 % time {catch {unset Q};Q' 30}
15633 microseconds per iterationRuntime of the non-cached version Q grows very exponentially, while the cached Q' runs in linear time (~510 usec - YMMV). So this is a case where result caching clearly pays off.
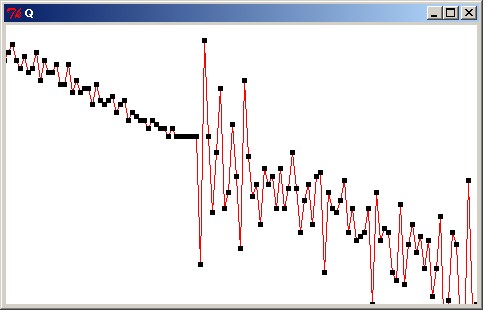
Now to visualize the results on a canvas - good-bye tclsh, hello wish. I draw a little black rectangle at every result of the Q function (positive y goes down as usual on a canvas, but this gives us a good diagonal irrespective of canvas size, so I didn't transform it). A red line connects the points - the Q function is not continuous, but this indicates how chaotic the values "burst" at certain times (in regular intervals), mostly so after a short stretch of constant values. The oscillations then slowly calm down again, but still not in an evident pattern...
For closer examination of the puzzling result sequence, zoom in with left, out with right mousebutton.
package require Tk
proc point {w x y {color black}} {
$w create rect [expr {$x-.5}] [expr {$y-.5}] \
[expr {$x+.5}] [expr {$y+.5}] -fill $color
}
pack [canvas .c -bg white] -fill both -expand 1
set line [.c create line 0 0 0 0 -fill red]
for {set i 1} {$i<800} {incr i} {
point .c $i [Q' $i]
.c coords $line [concat [.c coords $line] $i [Q' $i]]
update
}
bind .c <1> {.c scale all %x %y 2 2}
bind .c <3> {.c scale all %x %y .5 .5}
bind . <Escape> {exec wish $argv0 &; exit}
bind . <?> {console show}rmax - Here is a version that runs about 30-40% faster by using [catch] instead of [info exists] and referencing the cache variables in the global namespace instead of using [global]:
proc Q4 n {
if {[catch {set ::Q4($n)}]} {
if {$n<=2} {
set ::Q4($n) 1
} else {
set ::Q4($n) [expr {[Q4 [expr {$n - [Q4 [expr {$n - 1}]]}]]
+ [Q4 [expr {$n - [Q4 [expr {$n - 2}]]}]]}]
}
}
set ::Q4($n)
}The next one embeds the two [if]s into the expressions and gains another 3% in speed at the cost of readablilty:
proc Q5 {n} {
expr {[catch {set ::Q5($n)}]
?[set ::Q5($n) [expr {$n<=2 ? 1:
[expr {[Q5 [expr {$n - [Q5 [expr {$n - 1}]]}]] +
[Q5 [expr {$n - [Q5 [expr {$n - 2}]]}]]}]}]]
:$::Q5($n)
}
}If we preallocate the array indexes up to the recursion limit of the interpreter and put in the values for Q(1) and Q(2) the function becomes a lot easier and another 45% faster.
for {set i 0} {$i <= [interp recursionlimit {}]} {incr i} {
set Q6($i) 0
}
array set Q6 {1 1 2 1}
proc Q6 {n} {
expr {$::Q6($n) ? $::Q6($n) :
[set ::Q6($n) [expr {[Q6 [expr {$n - [Q6 [expr {$n - 1}]]}]] +
[Q6 [expr {$n - [Q6 [expr {$n - 2}]]}]]}]]}
}
# And now we fill the cache...
Q6 [interp recursionlimit {}]
# ... and turn the function into a lookup table
proc Q6 {n} {set ::Q6($n)}Lars H: An implementation using bifurcation:
proc Qb {n} {
array set cache {1 1 2 1}
bifurcation [list $n] {n} {
if {[info exists cache($n)]} then {
set cache($n)
} else {
spawn Qm1 [expr {$n-1}]
spawn Qm2 [expr {$n-2}]
}
} {Qm1 Qm2} {
spawn Qn1 [expr {$n - $Qm1}]
spawn Qn2 [expr {$n - $Qm2}]
} {Qn1 Qn2} {
set cache($n) [expr {$Qn1 + $Qn2}]
}
}In this case, the function values are cached in a local array (thus no memory leak). It also isn't subject to the recursion limit.
Qb 20000
is quite possible (although not all that fast); the value is 10199.
DKF: Rewriting to use the mathfunc syntax:
proc tcl::mathfunc::Q n {
expr {
$n <= 2 ? 1 : Q($n - Q($n - 1)) + Q($n - Q($n - 2))
}
}
proc Q n {expr {Q($n)}} ;# Convenience onlyThat's prettier, but would need memoization to be fast.
# Simpler to populate the cache with the base case
set Q {--> 1 1}
proc tcl::mathfunc::Q n {
global Q
if {$n >= [llength $Q]} {
lappend Q [expr { Q($n - Q($n - 1)) + Q($n - Q($n - 2)) }]
}
return [lindex $Q $n]
}Note that the straight lappend works fine; a feature of this function is that for any N (> 2), if you want to calculate Q(N) you need to first calculate Q(N-1) and you never need to calculate Q(M) where M ≧ N. These guarantee the safety of the use of lappend.