Human Language Root Words & Lexicostatistics Calculator and eTCL Slot Calculator Demo Example, numerical analysis
Human Language Root Words & Lexicostatistics Calculator and TCL Slot Calculator Demo Example
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold
- Human Language Root Words & Lexicostatistics Calculator and TCL Slot Calculator Demo Example
- Introduction
- Notes on 3 Keltic Invasions of Europe
- Appendix Code
- Comments Section
Introduction
gold Here is some TCL starter code on a calculator for human language root words. The impetus for these calculations was checking some references in Sumerian and cuneiform mathematics. Most of the testcases involve experiments or models, using assumptions and rules of thumb.
The original formulas were developed by Morris Swadesh in the changes of native American languages, published 1950 to 1955. Swadesh published a lexical constant fraction of 0.86 in 1955, restating that 86% of original root words should remain in a source language after 1000 years. In the various papers, Swadesh used selected word lists of 215, 200, and 100 root words. The original formula was N(t) = N(0)*exp(-lambda*t). In TCL notation, the remaining root words N2= [*kay [/ N1 [exp [/ $t 1000.]]]]], where N1 is the original set of root words, 1000. years for millennium, and t is the time in years. The constant kay equals [* [/ 86. 200.] [exp 1. ]]] or 1.16886, where [exp 1. ]]] is familiar natural number 2.718. As a rule of thumb, a second language with different roots of 50 percent is not easily understandable from a first or source language, and probably would be considered a second language. There might be 5 percent error in comparison lists of two languages, so the 50% criterion from the rule of thumb can be relaxed somewhat. In modeling a descendant language from a source language, the criterion is postulated that a language with more than 46 percent of root words remaining is a descendant of the source language.
For the TCL calculator, one enters time in years, number of root words in list at time zero (usually 200), and the remaining root words after time. Using the Swadesh formula and constant of 86, the minimal or predicted number of remaining root words is estimated. The decimal fraction of remaining words would be [/ N2 N1] and the percentage of remaining root words after time would be [* [/ N2 N1] 100.]. The TCL calculator can report if more than 46 percent of root words is passed as a criterion, suggesting that the second language set (remaining roots) is a descendant language. The TCL calculator can report if { $percent >= 46. } { set passfaillogic 1. }, 1 for yes or 0 for no. If the remaining root words after time is not known accurately, one can reload the predicted number as roots2 and push solve a second time for tentative lower bound. For example in testcase 4, the TCL calculator returned a percentaqe of 60 percent for 120 remaining root words, but less accuracy. Reloading the minimal 85 root words, the TCL returned 42.5 percent. So the lower/upper bounds on the solution would be 42 to 60 percent.
A related formula that Swadish used was separation time in millennia equals (ln C) / (2* (ln R) ), where C is the fraction of roots words that two languages have in common and R is the Swadesh ratio (0.86). The separation time is an estimate of when two related languages separated from a common source language before present (BP). For example, an early study found that the French and German languages have 33% root words in common or decimal ratio 0.33. The separation in years would be (ln C) / (2* (ln R) ), ln(.33)/(2*ln(.86)) =-1.1086 / (2*-.1508), or 3.675 millennia before present (BP).
A more sophisticated analysis of the F&G separation indicated the common roots of F&G at fraction 0.351 and 35.1 percentage. One error source was the limited vocabulary lists of 200 or so, which introduce a quantization error of about [- 1 [/66 67]]] or 1 percent for each word in error. From the 200 word list tallies, each word in error means that the separation formula estimates about 50 years per word in error. Overall, there was about a 15 percent error in the linguistic calculations. Consequently, the time of separation between F&G was between 3400 and 4200 years BP. One historical event that took place near the F&G separation was the volcanic eruption of the island of Thera in 1475 BCE or 3489 BP. Other papers suggest the Minoan eruption of Thera took place near 1628 BCE based on tree rings and near 1613-1660 BCE based on carbon dating. It has been speculated that the volcanic dust, crop failures, and poor grassland yields damaged the ecology of the Middle East and triggered one of the Celtic or Indo-European invasions of Europe.
Continuing with the eTCL calculator on the separation of French and German, one loads 200 root words for time zero and 66 words as remaining roots. The solved ratio would be [/ 66 200] or 0.33 as above for the common roots of French and German. The eTCL notation for years separation would be set separation [* 1000. [/ [log $newratio ]]] [* 2. [log .86 ]]]]] years BP. This function for separation was loaded into the calculation routine, but can be pasted into the eTCL console. The fraction 0.33 estimated the years of separation as 3675 before present or 1661 BCE +-200 years. For another bound on the F&G separation, the fraction 0.351 or 70/200 was returned in the separation formula as 3480 years BP or 1466 BCE , +-200 years. While quantization error was not the only error, the quantization error on the two calculations can be estimated as [* 50. [70-66]]] or 200 years. This added separation function shows how the calculator can be modified, but the separation function should be handled carefully since the interpretation and derivation of the separation function is a little different.
Ironically, the first estimate for the F&G separation at 1661 BCE +-200 years was in close agreement within the bounds of tree ring estimates and carbon 14 dates. For the first estimate, the reported error of +-200 years was based on the 200 word lists. The analysis might point out that reducing the wordlist from 200 to 100 root words substantially increases the quantization error. The quantization error from a hundred word list would be [- 1 [/ 33 34]]] , 3 percent quantization error for each word. Continuing with 4 words in error, the total error on the F&G problem would be 12 percent (+-400 years) using the 100 word list. The conclusion is that human languages change over the years. If there are N1 number of roots in the source language, there will be some smaller fraction N2 left over the years.
Table 1 : Swadesh Constants and Separation of F&G
| Swadesh Constants and Separation of F&G | table printed | in tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| first estimate F&G separation | 1661 BCE | first cut, used common root fraction 0.33, +-200 years |
| second estimate F&G separation | 1466 BCE | used common root fraction 0.351 |
| Minoan volcanic eruption of Thera | 1475 BCE | used chronology of Egyptian Kinglist primarily |
| Minoan volcanic eruption of Thera | 1618 BCE | used carbon dating from Thera and Knossos palace |
| Minoan volcanic eruption of Thera | 1620-1660 BCE | used Canadian tree rings and Californian bristle pines |
| Possibly more than one volcanic eruption of Thera | 1450-1660 BCE | in period of interest. |
| Swadesh-200 fraction | 0.81 decimal | used with list of 200 root words, Swadesh original use |
| Swadesh-200 constant | 81 percentage | used with list of 200 root words, Swadesh original use |
| Swadesh-200 lambda | 0.19 | 1.-lambda(0.19)=0.81, [exp [*-1. $lambda $t]]] Swadesh original use |
| Lees-200 fraction | 0.805 decimal | used with list of 200 root words, Lees revised use of 0.805 +- 0.0176 with 90% confidence |
| Lees-200 constant | 80.5 percentage | used with list of 200 root words, Lees revised use |
| Lees-200 lambda | 0.195 | used with list of 200 root words, Lees revised use |
| Swadesh-100 fraction | 0.86 decimal | used with list of 100 root words, Swadesh revised use |
| Swadesh-100 constant | 86 percent | used with list of 100 root words, Swadesh revised use |
| Swadesh-100 lambda | 0.14 | 1.-lambda(0.14)=0.86, [exp [*-1. $lambda $t]]]Swadesh revised use |
| years of separation, ref. Swadesh | [* 1000. [/ log $newratio ] [* 2. [log .86]] years BP | root words common to F&G over source |
| years of separation, ref. Swadesh | [- [* 1000. [/ log $newratio ] [* 2. [log .86]] $current_year ] years BCE | years separation rated to BCE |
Notes on 3 Keltic Invasions of Europe
Question?: Do you have date or century info on the Kelt invasions of Europe. Possibly more than one invasion? One invasion by Kelts was apparently triggered by the volcanic destruction of Thera in 1475 BCE, better known as Atlantis?
M.C. forwards reply and following content of human genetic evidence on Keltic invasions in Europe.
1) The first invasions of Europe by one group of ancestors of the Kelts took place already between 5000 BC and 4500 BC from the East Steppes towards the West Steppe and into Western Europe.The Greek line Kelts that you talk about would have been Y-DNA R1b-L23 (Copper and Bronze Age Maykop) etc. bringing with them Y-DNA J2a people from Greece and the Caucasus during the Neolithic. The second invasion including ongoing movement inside Europe already may be accounted with the R1b-L21 (Celt-Gael) descendants in roughly 2000 BCE to 500 CE. The R1b-L21 (Celt-Gael) descendants moved into Ireland and other British parts between 2000 BC and 1000 BC-500 AD. The other R1b-P312 old strains they found in Scotland were from Celtic families who went straight over to Britain in 2300-1200 BC. The 3rd group of Celts were G2a3 people who came from the Caucasus and G2a4 European Neolithics and were later part of the society created by I2a and R1b Celts at Hallstatt, (1200 BC). Archeological remains at Hallstatt (1200 BC) appears to be closest to cited volcanic activity on island of Thera and within expected error bounds. Invasion across the Bosperous straits would have been problematic for these Kelts in 1475 BCE, so the Macedonia-Balkans area seems plausible as a starting point and land route for the third Keltic group into Europe. Believe the human genetic research adds considerable depth to the human root word findings.
2) In human genetics, Haplogroup R1b is the most frequently occurring Y-chromosome haplogroup in Western Europe, Bashkortostan 3 and in parts of sub-Saharan Central Africa (for example around Chad and Cameroon). R1b is also present at lower frequencies throughout Eastern Europe, Western Asia, Central Asia, parts of North Africa.Single-Nucleotide Polymorphisms (SNPs) are very stables, mutating rarely. Most European R1b paternal lineages are related within the last several thousand years. That means that R1b STR based haplotypes often look alike. The most common pattern of Y STRs is the Western Atlantic Modal Haplotype (WAMH). Most R1b people match several components of it. It is just a remnant of the fact we are closely related. SNPs differentiate the branches of R1b’s descendants tree. C1 in Europe was the oldest haplogroup there. C1 displaced by Y-DNA I2 men in Paleo or Ice Age when this started. C1 still left further east in East Europe, but there C1, H2 were displaced by the Ind-European R1a groups.
3) One group of Greeks who became Kelts entered Ireland at the same time as the R1b-L23 people and R1b-L21 group. The Greek group 1 Kelts were Y-DNA J2a3b or something. The other group was a J2b. There are more J2a types left in Britain than the J2b group of Greeks. Very small % today. The main group of Kelts who invaded Europe were origianlly actually ancestors of the Kelts - R1b - R1b-P312 . A small Sarmatian type group Cimmerians were R1b-L23. Some Greeks were Trojan R1a (Slav-like) and another Greek group was their tribute clan E1b1 from south Greece.
4) The 3rd group of Celts were G2a3 people who came from the Caucasus and G2a4 European Neolithics and were later part of the society created by I2a and R1b Celts at Hallstatt, (1200 BC). The original leaders of the invading Keltic groups from Greece and the Steppe into Europe were R1b. There were some I2a Balkan leaders with them from the Balkans. There were also local I2a people in West Europe already who were Mesolithic henge people
5) R1b is the paternal branch of the human family tree marked by the mutation M343+. R1b includes all R-M269 people. If you are R1b of any type, including predicted M343+, P25+, M269+ or of any descendant SNP such as U106+, P312+, L21+, DF27+, U152+, S1194+, Z2103+ or V88+ But there were two mutations one for red hair and one for blonde hair in this group and two mutations of autosomal DNA carried by the R1a group. R1a was already in parts of the Balkans by then (Neolithic late - 5000 BC) and the first R1b groups to be inEurope were R1b-DF types. These were spin offs, like R1b-V88 from the original Haplogroup R1b (R-M343), (Bashkir)Greco-Anatolian, Italic, Celtic and Germanic branches of the Indo-European speakers. France and West Europe in Paleolithic and Mesolithic inhabited by C1 (very few left), H2 (few left), G2a4 (Neolithic hunter-farmers-with axe technology ) and some I2a people.
6) The Greek line Kelts that you talk about would have been Y-DNA R1b-L23 (Copper and Bronze Age Maykop) etc. bringing with them Y-DNA J2a people from Greece and the Caucasus during the Neolithic.
7) The oldest group of Britons were similar to the old Irish Mesolithic group of 7000 BC - I2a (men) . The Viking groups who later invaded the parts of Caithness and Sutherland in 700-800 AD were I1a. I1a is the old Skandza group of South Sweden and spread into the Balkans. The R1b-L21 (Celt-Gael) descendants moved into Ireland and other British parts between 2000 BC and 1000 BC-500 AD. The other R1b-P312 old strains they found in Scotland were from Celtic families who went straight over to Britain in 2300-1200 BC.
Related post:
8) R1b-P312 had about 3 descendant mutations R1b-L51- which later had another mutation to R1b- L21 (Gaels)- . The cousin mutation of the P312 was a branch of R1b-U106 which became ancestors of some North Sea Germanic (Angles). Angles had two groups. One group was an unrelated Megalomose Culture People Y-DNA I1a (Cro-Magnons with a bump on top of the head ). The second group of Angles were from Indo-European stock [R1b-U106). The one group of Franks were R1b-U105.
9) Invasion from the steppe, Caucasus and Anatolia by a Y-DNA R1b group R1b-M269 and their women they took with them into where modern Belarus and Ukraine are. There were already earlier groups there (a Proto-Slavic R1a paternal group) when R1b arrived there. The mutation for the North Atlantid Keltid Y chromosome's ancestor was taking place within a group that was an ancestor of the Italic-Celtic-Germanic R1b bloodstrains - which became R1b-P312. End of genetic content.
gold 7/15/2020. based on Wikipedia. Note on 6) above. In medieval Irish myth, the Fir Bolg are the fourth group of people to settle in Ireland. The Fir Bolg are descended from the Muintir Nemid and were called the "men of bags" or "bag men" . Those Kelts who went to Greece became the Fir Bolg and eventually moved to Ireland. The legend is that the Fir Bolg were either captured soldiers or workers. The Greeks made them carry heavy bags and serve in the Greek armies. After ruling Ireland for some time, the Fir Bolg or men of the bag are overthrown by the invading Tuatha Dé Danann.
Pseudocode Section
pseudocode can be developed from rules of thumb.
pseudocode: enter time in years, number of remaining root words
pseudocode: output fraction of (remaining root words) over (root words at time zero)
pseudocode: output remaining root words as fraction
pseudocode: rules of thumb can be 3 to 15 percent off, partly since g..in g..out.
pseudocode: need test cases > small,medium, giant
pseudocode: need testcases within range of expected operation.
pseudocode: are there any cases too small or large to be solved? Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
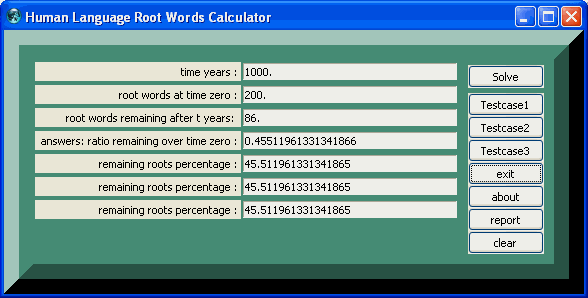
Testcase 1
| ancient language | table printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 1 | |
| time in years at time zero : | 1000. | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 86. | |
| answers: min. remaining root words from formula : | 85.0 | |
| ratio remaining root words : | 0.43 | |
| remaining root words percentage: | 43.0 | |
| language descendant criterion > 46% (0 or 1) : | 0. | logic variable, 1 for yes, 0 for no |
Testcase 2
| ancient language 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 2 | |
| time in years at time zero : | 1000. | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 120. | |
| answers: min. remaining root words fm formula : | 85.0 | |
| ratio remaining root words : | 0.6 | |
| remaining root words percentage: | 60.0 | |
| language descendant criterion > 46% (0 or 1) : | 1. | logic variable, 1 for yes, 0 for no |
Testcase 3
| ancient language 3 | table printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 3 | |
| time in years at time zero : | 1000. | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 160. | |
| answers: min. remaining root words from formula : | 85.0 | |
| ratio remaining root words : | 0.8 | |
| remaining root words percentage: | 80.0 | |
| language descendant criterion > 46% (0 or 1) : | 1. | logic variable, 1 for yes, 0 for no |
Testcase 4
| ancient language and lower bound calculation | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 4 | |
| time in years at time zero : | 1000. | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 120. | |
| answers: min. remaining root words from formula : | 85.0 | |
| ratio remaining root words : | 0.6 | |
| remaining root words percentage: | 60.0 | |
| minimal roots 85 reloaded to establish lower bound | ****** | ****** |
| time in years at time zero : | 1000. | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 85. | |
| answers: min. remaining root words from formula : | 85.0 | |
| ratio remaining root words : | 0.425 | |
| remaining root words percentage: | 42.5 | |
| language descendant criterion > 46% (0 or 1) : | 0. | logic variable, 1 for yes, 0 for no |
| percentage lower to upper bounds : | 42% to 60% |
Testcase 5
| First estimate, years of separation between F&G | table printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 5 | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 66. | |
| ratio remaining root words : | 0.33 | |
| remaining root words percentage: | 33.0 | |
| language descendant criterion > 46% (0 or 1) : | 0. | logic variable, 1 for yes, 0 for no |
| year separation before present BP : | 3675 | error +- 200 years |
| year separation BCE : | 1661.379 | error +- 200 years |
| conclusion: | possibly Minoan eruption of Thera volcano near 1613-1660 BCE, based on carbon dating | example needs check |
Testcase 6
| Second estimate, years of separation between F&G | table printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 6 | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 70. | |
| answers: min. remaining root words fm formula : | 86.0 | |
| ratio remaining root words : | 0.35 | |
| remaining root words percentage: | 35.0 | |
| language descendant criterion > 46% (0 or 1) : | 0. | logic variable, 1 for yes, 0 for no |
| year separation before present BP : | 3480 | error +- 200 years |
| year separation BCE : | 1466 | error +- 200 years |
Testcase 7
| Separation between Latin(200CE) and Spanish(2014CE) | table printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 7 | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 131. | from 200*0.655 |
| ratio remaining root words : | 0.655 | |
| remaining root words percentage: | 65.5 | |
| language descendant criterion > 46% (0 or 1) : | 1. | logic variable, 1 for yes, 0 for no |
| years separation before 2014CE: | 1402.705 | error +- 200 years |
| year of separation CE : | 611CE | error +- 200 years |
| conclusion: | possibly Muslim invasion of 711CE | example needs check |
Testcase 8
| Separation between Greek Koine(250BCE) and Cypriot(2014CE) | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 8 | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 135. | |
| answers: min. remaining root words fm formula : | 86.0 | |
| ratio remaining root words : | 0.675 | |
| remaining root words percentage: | 67.5 | |
| language descendant criterion > 46% (0 or 1) : | 1. | logic variable, 1 for yes, 0 for no |
| year separation before present BP : | 1303 | error +- 200 years |
| year separation CE : | 711 CE | error +- 200 years |
| conclusion: | possibly Arab raids on Cyprus, 700-800CE | example needs check |
Testcase 9
| Separation between Sung Dynasty Chinese(950CE) and Mandarin(2014) | table printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| testcase number | 9 | |
| root words at time zero: | 200. | |
| root words after time (t2-t0) : | 159 | |
| answers: min. remaining root words fm formula : | 86.0 | |
| ratio remaining root words : | 0.795 | |
| remaining root words percentage: | 79.5 | |
| language descendant criterion > 46% (0 or 1) : | 1. | logic variable, 1 for yes, 0 for no |
| year separation before present BP : | 760 | error +- 200 years |
| year separation CE : | 1253 | error +- 200 years |
| conclusion: | possibly Genghis Khan invests Peking (1214CE) | example needs check |
Screenshots Section
figure 1.
References:
- Lexicostatistics, google search
- ABC's of Lexicostatistics, Sarah C. Gudschinsa
- Thera [L1 ]
- Classificatiion of the Frisian Dialects, Petra Novotna & Vaclav Balzek
- PLoS One. 2013; 8(8): e71004.
- Environmental Roots of the Late Bronze Age Crisis
- Michael D. Petraglia, Editor, well worth reading
- Toward a phylogenetic chronology of ancient Gaulish, Celtic, and Indo-European
- Peter Forster and Alfred Toth
Appendix Code
appendix TCL programs and scripts
# TCL source code follows
# pretty print from autoindent and ased editor
# human language root words calculator V2
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL Club, 2Dec2018
package require Tk
namespace path {::tcl::mathop ::tcl::mathfunc}
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { time years :} }
lappend names { root words at time zero :}
lappend names { root words remaining after t years: }
lappend names { answers: minimum remaining root words from formula :}
lappend names { ratio remaining roots over roots1(t=0):}
lappend names { remaining roots percentage :}
lappend names { language descendent criterion > 46% (0 or 1) :}
foreach i {1 2 3 4 5 6 7} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg " Human Language Root Words Calculator V2
from TCL
# gold on TCL club , 2Dec2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Human Language Root Words Calculator V2
from TCL ,
# self help listing
# 3 givens follow.
1) time years
2) root words at time zero
3) root words remaining after t years
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# >>> copyright notice <<<
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers
# retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
# gold on TCL Club, 2Dec2018 "
tk_messageBox -title "Self_Help" -message $msg }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 testcase_number
incr testcase_number
set years $side1
set roots1 $side2
set roots2 $side3
set exponent [/ $years 1000.]
set kay [* [/ 86. 200. ] [exp 1. ]]
set calcroots2 [/ [* $roots1 $kay ] [exp 1 ] ]
set newratio [/ $calcroots2 $roots1 ]
set newratio [/ $roots2 $roots1 ]
set percentx [* $newratio 100. ]
set passfaillogic 0.
if { $percentx >= 46. } { set passfaillogic 1. }
set calcroots2 [* [int $calcroots2 ] 1. ]
set side4 $calcroots2
set side5 $newratio
set side6 $percentx
set side7 $passfaillogic
return $side7 $passfaillogic
}
proc fillup {aa bb cc dd ee ff gg} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"}
proc clearx {} {
foreach i {1 2 3 4 5 6 7} {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 testcase_number
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Human Language Root Words , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%| table |printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number| $testcase_number||& "
puts "&| time in years at time zero :| $side1 ||&"
puts "&| root words at time zero:| $side2 ||& "
puts "&| root words after time (t2-t0) :| $side3 ||& "
puts "&| answers: min. remaining root words fm formula :|$side4 ||&"
puts "&| ratio remaining root words :| $side5 ||& "
puts "&| remaining root words percentage:| $side6 ||&"
puts "&| language descendant criterion > 46% (0 or 1) :| $side7 ||&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1000. 200. 86. 85.0 0.43 43. 0. }
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1000. 200. 120. 85.0 0.6 60. 1. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1000. 200. 160. 85.0 0.8 80. 1. }
::ttk::button .clearallx -text clear -command {clearx
}
::ttk::button .about -text about -command { about }
::ttk::button .self_help -text self_help -command { self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Human Language Root Words Calculator V2"
Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers (which numbers will be cleared on the next solve button.) The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
gold This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here, Thanks.