A not-so-random path based on primes
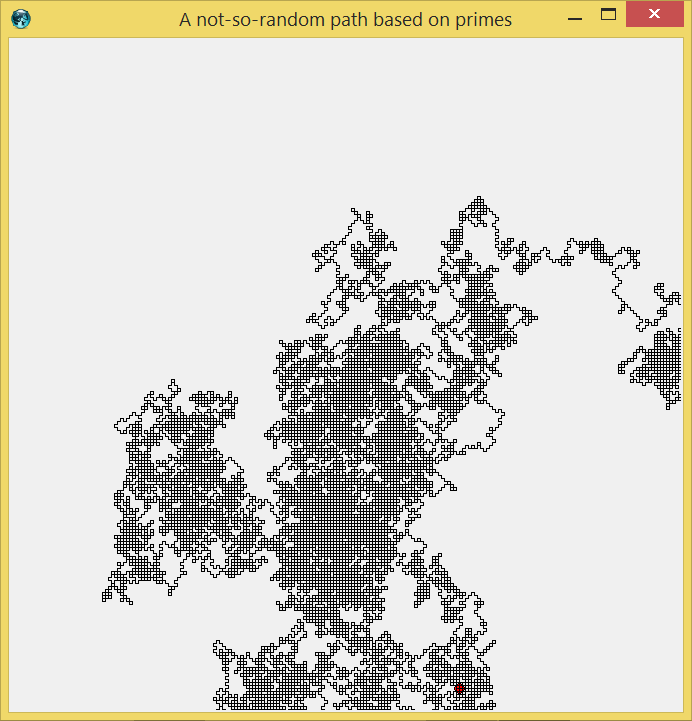
Arjen Markus (15 july 2013) A newspaper article this weekend inspired me to this little program. The author used prime numbers to decide where to go next. That is: take the second turn, then take the third, then the fifth and so. Roundabouts, culs-de-sac and one-way streets made it more difficult than you might think at first, but that is reality playing cat-and-mouse.
On a canvas, there is no such difficulty.
Well, I did have a tiny problem: if you let the step size for the next step depend linearly on the prime, then you need a very big canvas or you need to scale. So, instead I simply take steps of three pixels and the direction depends on the prime number. What scheme you use for turning a prime into a direction determines in an unpredictable (?) way what path you get.
I have preprogrammed four methods, but it is very easy to come up with others. Small reminder: primes larger than 3 are all of the form 6n+1 or 6n+5. And all primes larger than 2 are of the form 4n+1 or 4n+3. Two little facts I use in the program below.
One note: to select the type of path, set the variable type to 0, 1, 2 or 3.
# primetrail.tcl --
# Use prime numbers to generate a trail in a canvas
# Inspired by a newspaper article.
#
# The idea: draw a path in small steps where the direction
# and perhaps the step size depend on successive primes
#
#
# Four types:
# 0 - Based on mod 6: the path turns left or right, depending on p%6
# 1 - Based on mod 5: the path goes north, west, south or east, based on p%5
# 2 - Based on mod 5: the path turns over 0, 90, 180 or 270 degrees
# 3 - Based on mod 4: as mod 6
#
set type 0
package require math::numtheory
pack [canvas .c -width 800 -height 800]
set x 250
set y 250
set dirx 1
set diry 0
.c create oval 245 245 255 255 -fill red
if { $type == 0 || $type == 3 } {
set np 5
set mod [expr {$type == 0? 6 : 4 }]
} else {
set np 7
}
set p $np
for {set i 0} {$i < 50000} {incr i} {
if { $type == 0 || $type == 3 } {
if { $p%$mod == 1 } {
set ndirx [expr {$diry}]
set ndiry [expr {-$dirx}]
} else {
set ndirx [expr {-$diry}]
set ndiry [expr {$dirx}]
}
} elseif { $type == 1 } {
switch -- [expr {$p%5}] {
"1" {
set ndirx 0; set ndiry -1
}
"2" {
set ndirx -1; set ndiry 0
}
"3" {
set ndirx 0; set ndiry 1
}
"4" {
set ndirx 1; set ndiry 0
}
}
} else {
switch -- [expr {$p%5}] {
"1" {
set ndirx $ndirx; set ndiry $ndiry
}
"2" {
set ndirx [expr {-$diry}]; set ndiry $dirx
}
"3" {
set ndirx [expr {-$dirx}]; set ndiry [expr {-$diry}]
}
"4" {
set ndirx $diry; set ndiry [expr {-$dirx}]
}
}
}
set np [expr {$np%6 == 1? $np+4 : $np+2}]
set dirx $ndirx
set diry $ndiry
set nx [expr {$x + $dirx * 3}]
set ny [expr {$y + $diry * 3}]
#
# Note: you could use the prime to scale the step, but then
# the path quickly runs wild.
#
.c create line $x $y $nx $ny
set x $nx
set y $ny
while { ! [::math::numtheory::isprime $np] } {
set np [expr {$np%6 == 1? $np+4 : $np+2}]
}
set p $np
}
if { $type == 0 } {
.c move all 200 400 ;# Centre it, more or less
}
if { $type == 2 } {
.c move all 200 200 ;# Centre it, more or less
}gold added pix, random? looks like coasts of United Kingdom and Ireland