Making mathematical waves
When making sounds, the most fundamental way to create samples which represent pure and well defined waves is to use mathematically defined waves, for instance by explicit formulae as a function of time or sample number, assuming the samples are from a function of time with frequency spectrum limited to the Nyquist rate (half the sampling frequency). The latter is not completely true for the following example, but the spectrum is limited enough to give useful results.
This is where Tcl comes in to make a useful script which executes exactly the right commands to let us drive maxima and a dedicated C program to generate waveforms from powerful formulae. Not a very big script (not counting bwise along, because strictly speaking the below works mostly also without bwise) but one which calls two major applications (maxima and gcc), and which does the essential packing of a FORTRAN function in a suitable file, and finally automatically executes the compiled program, which writes a standard .wav file (see snack) to play with some media player.
Maxima can be integrated with Tcl in two main ways (see Calling Maxima from Tcl and Maxima through a pipe, and see also Bwise combined with Maxima). Here I use the easier programmable and memory friendly way to start up the executable from the Tcl (bwise) script.
This is the main Tcl script, which is combined with (sourced) bwise:
# Give some initialization to maxima, run it, and peel out the result
proc domaxima { {m} } {
set t "display2d:false;\n$m;"
return [string range [exec maxima << $t | tail -2 ] 6 end-7]
}
# Similar as above but get a FORTRAN converted result
proc domaximafor { {m} } {
set t "display2d:false;\nlinel:3000;\nfortran($m);\n"
return [string range [exec maxima -q << $t ] 42 end-18]
}
# Make the FORTRAN source file and compile
# and link it with the C main program, and run that.
proc formake { {e} } {
global f
set t [subst -nocommand {
subroutine sayhello(x,r)
real x,r
r = $e
return
end
}]
set f [open sub.f w]
puts $f [string trim $t \n]
close $f
exec gcc -ffixed-line-length-none -o fm sub.f mw.c wav.o -lm
#exec gfortran -ffixed-line-length-none -c sub.f
#exec gcc -o fm sub.o main.c -lm
return [exec ./fm]
} Of course maxima must be present on the system and reachable according to the PATH shell variable (like wish and tclsh). I've done this setup on Linux, which when set up right gives excellent maxima and compile times, with complicated formulas (see below) a long wav file is created in under a second (!). I guess this Tcl/maxima/FORTRAN/C setup is therefore useful for general application, too.
You need to have these files in the current directory which contains the wav file and C loop part of the target program:
/***** wav.c *****/
#include <stdio.h>
#include <fcntl.h>
#include <sys/stat.h>
#include <string.h>
#include <sys/types.h>
#include <stdlib.h>
/* #define CYGWIN */
int fd;
FILE *fp;
#define MSEC(t) (int)(t*44.1)
iwrite(fd,n,l)
int fd,l;
unsigned int n;
{
write(fd,&n,l);
}
int initwav(s,l) /* wav header, s=filename, l=#samples */
char *s;
int l;
{
#ifdef CYGWIN
fd = open(s,O_WRONLY|O_CREAT|O_TRUNC|O_BINARY,S_IRUSR|S_IWUSR|S_IRGRP);
#else
fd = open(s,O_WRONLY|O_CREAT|O_TRUNC,S_IRWXU);
#endif
if (fd < 0) return(-1);
write(fd,"RIFF",4);
iwrite(fd,(2*l+36),4);
write(fd,"WAVE",4);
write(fd,"fmt ",4);
iwrite(fd,(0x10),4);
iwrite(fd,((short) 0x01),2);
iwrite(fd,((short) 1),2); /* Mono */
iwrite(fd,(44100/1),4); /* Sample rate */
iwrite(fd,(2*44100/1),4);
iwrite(fd,((short) 2),2);
iwrite(fd,((short) 16),2);
write(fd,"data",4);
iwrite(fd,(2*l),4);
return(0);
}
void writewav(p,n)
short *p; /* Sample values */
int n; /* #samples */
{
int i;
for (i=0; i<n; i++)
write(fd,&p[i],2);
}
void closewav()
{
close(fd);
}
----
/****** mw.c ******/
/* This is file: main.c */
#include<stdio.h>
#include<math.h>
extern void sayhello_(float *, float *);
extern int initwav(char *,int);
extern int writewav(short *, int);
extern void closewav();
int main(argc, argv)
int argc;
char *argv[];
{
float in, out;
float x, start, stop, incr;
short s;
if (argc == 1) {
start = 0.0;
stop = 3.0;
incr = 1.0/44100.0;
if (initwav("math.wav",3*44100) != 0) return((int) -1);
for (x=start; x<(stop-incr/2); x+=incr) {
in = x;
sayhello_(&in,&out);
/* printf("%f %f\n", x, (float) out); */
s = (short) (32000*out);
writewav(&s,1);
}
closewav();
}
return((int) 0);
}Running the Tcl script with a complicated formula (using commands, not BWise blocks):
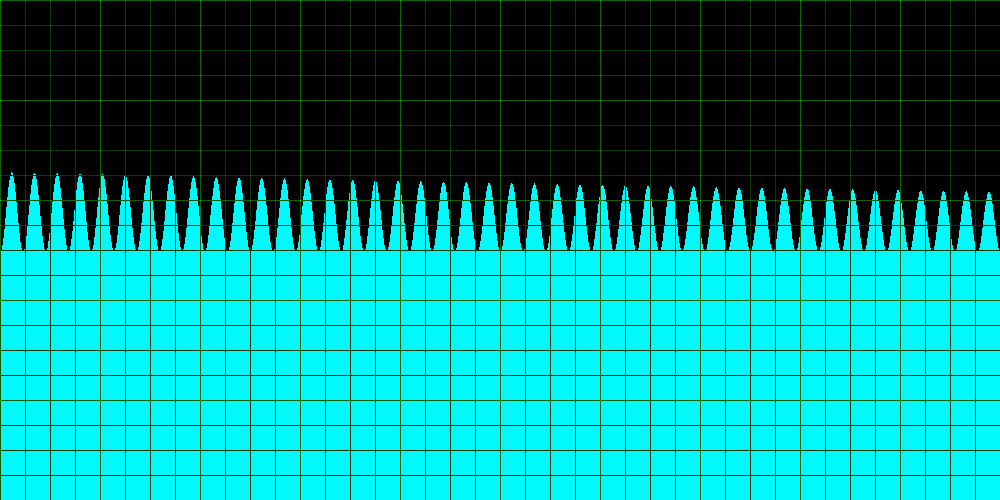
formake [domaximafor {(sin(6.2831*110*x)*exp(-2*x)+(1/2)*sin(2*6.2831*110*x)*exp(-4*x)+(1/3)*sin(3*6.2831*110*x)*exp(-6*x)+(1/4)*sin(4*6.2831*110*x)*exp(-8*x)+(1/5)*sin(5*6.2831*110*x)*exp(-10*x)+(1/6)*sin(6*6.2831*110*x)*exp(-12*x)+(1/7)*sin(7*6.2831*110*x)*exp(-14*x)+(1/8)*sin(8*6.2831*110*x)*exp(-16*x)+(1/9)*sin(9*6.2831*110*x)*exp(-18*x))/(1+(1/2)+(1/3)+(1/4)+(1/5)+(1/6)+(1/7)+(1/8)+(1/9))}]generates this FORTRAN file:
subroutine sayhello(x,r)
real x,r
r = 2.52E+3*(exp(-18*x)*sin(6.2202690000000002E+3*x)/9.0E+0+exp(-16*x)
1 *sin(5.5291279999999997E+3*x)/8.0E+0+exp(-14*x)*sin(4.837987000
2 0000001E+3*x)/7.0E+0+exp(-12*x)*sin(4.1468459999999995E+3*x)/6.
3 0E+0+exp(-10*x)*sin(3.4557050000000004E+3*x)/5.0E+0+exp(-8*x)*s
4 in(2.7645639999999999E+3*x)/4.0E+0+exp(-6*x)*sin(2.073422999999
5 9998E+3*x)/3.0E+0+exp(-4*x)*sin(1.3822819999999999E+3*x)/2.0E+0
6 +exp(-2*x)*sin(6.9114099999999996E+2*x))/7.129E+3
return
end
And this [L1 ] is the resulting wav file, its a 260 kilobyte 16 bit wav file.
Part of he formula in neater form: 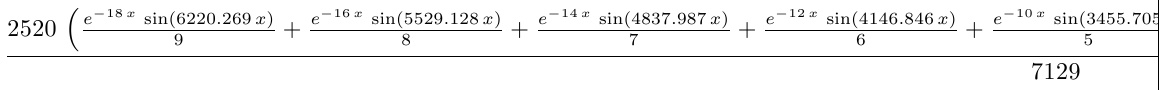
Finally, it is also possible to read the resulting wav file in a sampler or sample software and 'play' it with different keys on a (USB or midi) keyboard, which is great fun.
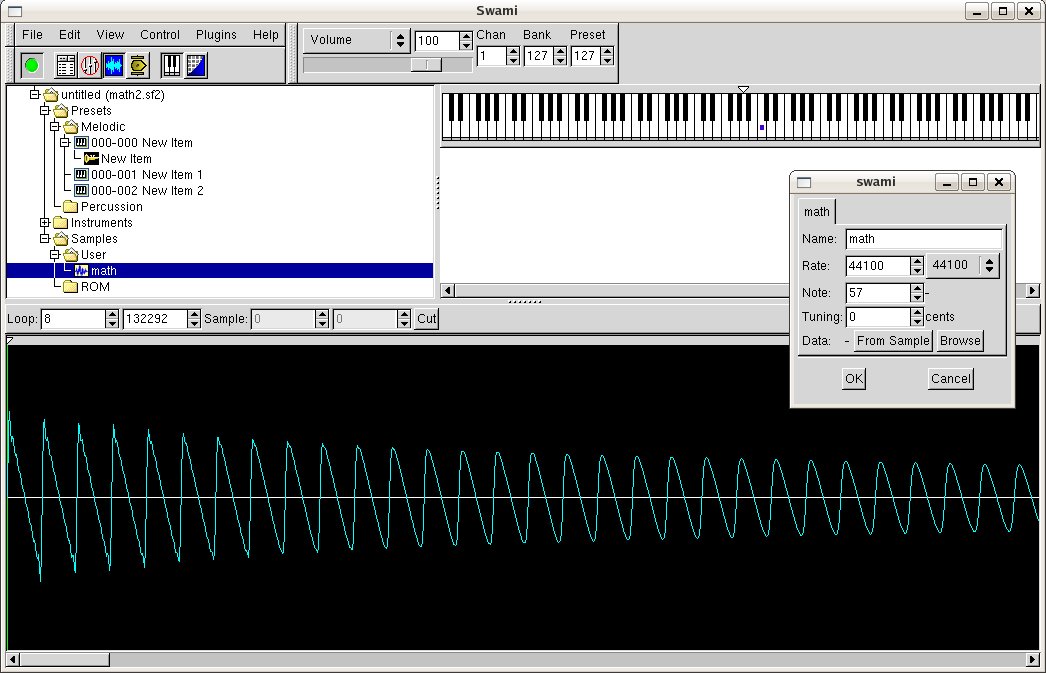
I've used the open source swami program to make a soundcanvas from the sample, in principle a multi sample can also be created this way:
I'd like a Tcl script or package, or integrable command line utility to make soundcanvasses under Tcl control..
Versions of the software used are: Tcl version 8.4 on Linux Redhat Fedora core 5, gcc 4.1.0, Maxima 5.12.0-3.fc5, Bwise 0.343 with console for Unix (,swami 0.9.4, fluidsynth 1.0.7). See also a Tcl script for function value listing based on a FORTRAN expression. I recently also used FC6/64 with Tcl 8.4, Maxima 5.12.0 , gcc 4.1.1 .
As a side remark: in Electrical Engineering and various other disciplines the above type of combined exponential / sine terms are very important and fundamental types of formulas which arise as the solution to important network theoretical linear but reactive circuits or systems differential equations.
Needless to say, because of the block facilities or bwise and general Tcl/Tk possibilities, a powerful environment can be made.
Maybe I'll put an example here of a block based formula rendering.
TV Aug 28 '08 I've made the approach work fairly ok with the tcl scripts described here: apache server with tcl cgi scripts running on safe user alhough extensive multiuser work has not been tested, and might send the server into overtime work...
I made a good improvement by getting gnuplot called from maxima called from the main server tread of the cgi script chain and replacing the repeated call to the Maxima executable with a large memory space claiming exec call by an addition to the main (runtime gcc compiled) C/Fortran program, where a similar 0.1 second graph of 500x1000 pixels is made in C, written as .ppm file, and converted to .gif, which takes a lot less time: the C program is efficient in time and memory and so now the whole page solving a new formula and rendering it takes usually under 3 seconds to complete, with prettyprinting, graph, and sound files being made.
The C code can be found here [L2 ] for those who want to experiment, and the tcl script code has certain execs commented out. The resulting graph (in this hacked version) looks like this:
Feel welcome to try some simple or difficult examples, for instance like this one:
http://82.171.148.176/cgi-bin/maxwav.tcl?rhs(ic1(ode2((x+1)^2*'diff(y,x)+3*y*(x+1)=440*sin((x+1)*2*%pi*440)/(x+1),y,x),x=0,y=0))
N.B. Pressing the link probably won't work because the auto-link forgets the last two ))'s
which is instructing maxima over the 3 tcl wen scripts to solve a second order differential equation formally, and then the sound becomes like this: [L3 ]
I've also made mid file renderings with mathematical waves from the program described on the other page I mentioned above, where the result is free from any of the modern mess that al kinds of transforms and sampling artifacts have all the time, and therefore very musical.
I'll think about making a package of the required programs (minus the C compiler, which could better be fast like gcc with ramdisk on a good linux machine), so that in combination with bwise interesting wave and signal processing research is possible. Oh yeah, and the fortran scene has made a frienly attempt to improve things by making an non-backward compatible main math library change which makes it necessary to update your compiler when you get a new fortan part.
TV the server link (nowadays www.theover.org/...) isn't active. If someone would like to play with it, I could put it on the current server, just ask.