Cubic Function Explorer
Keith Vetter 2006-12-18 : Here's a little program that plots cubic equations. It lets you tweak the values for the four terms. I saw this as an applet and thought it would make a fun little afternoon programming exercise.
uniquename 2013aug18
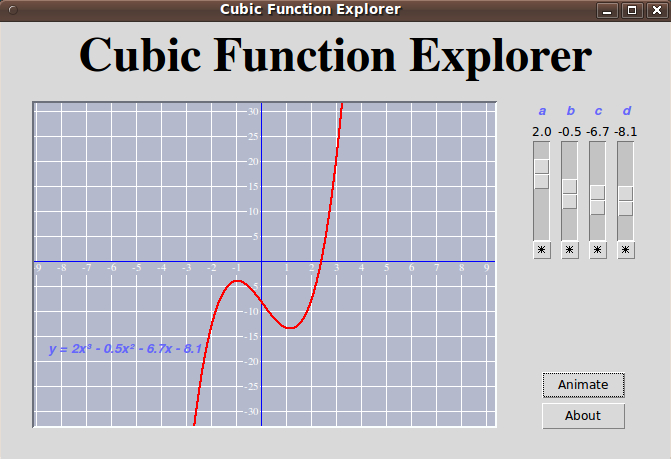
For those readers who do not have the time/opportunity/facilities/whatever to run the code below, here is an image that shows the nice-looking, nice-performing GUI that the code produces.
In 'Animate' mode, the sliders for the 4 coefficients automatically advance through their ranges (left-most scale moving fastest).
As the scales change, the curve updates (moves) immediately, and the coefficients of the equation shown on the graph updates just as fast. In 'Animate' mode, the curve and the equation coefficients are updating 'like crazy' (i.e. fast) --- and that's on my little netbook computer that people insist is too weak to do anything but function as a paper weight or door stop.
Jeff Smith 2021-03-23 : Below is an online demo using CloudTk. This demo runs "Cubic Function Explorer" in an Alpine Linux Docker Container. It is a 27.4MB image which is made up of Alpine Linux + tclkit + Cubic-Function-Explorer.kit + libx11 + libxft + fontconfig + ttf-linux-libertine. It is run under a user account in the Container. The Container is restrictive with permissions for "Other" removed for "execute" and "read" for certain directories.
##+########################################################################## # # cubic.tcl -- Displays the graph of some cubic equations # by Keith Vetter, December 2006 # # http://www.mathopenref.com/cubicexplorer.html package require Tk package require tile array set S {title "Cubic Function Explorer" X 25 Y 5 bg #b4bacc eq #6466fc go 0 delay 75} array set MAX {a 4 b 5 c 25 d 25} array set DIR {a 1 b 2 c 5 d 5} foreach who {a b c d} { set C($who) [expr {-$MAX($who) + int(rand()*2*$MAX($who))}] } proc DoDisplay {} { global S MAX wm title . $S(title) label .title -text $S(title) -font {Times 36 bold} frame .ctrl canvas .c -relief sunken -bd 2 -bg $::S(bg) foreach who {a b c d} { label .ctrl.l$who -text $who -font {Helvetica 10 italic bold} -fg $S(eq) label .ctrl.v$who -textvariable ::C(nice,$who) -width 3 ::ttk::scale .ctrl.s$who -from $MAX($who) -to -$MAX($who) \ -variable ::C($who) -orient v -command NewValue ::ttk::button .ctrl.z$who -image ::img::star -command [list Zero $who] \ -takefocus 0 } ::ttk::button .anim -text Animate -command StartStop ::ttk::button .about -text About -command About pack .title -side top -fill y pack .ctrl -side right -fill y -pady {10 30} -padx {0 30} pack .c -side left -fill both -expand 1 -pady {10 30} -padx 30 grid .ctrl.la .ctrl.lb .ctrl.lc .ctrl.ld grid .ctrl.va .ctrl.vb .ctrl.vc .ctrl.vd grid .ctrl.sa .ctrl.sb .ctrl.sc .ctrl.sd grid .ctrl.za .ctrl.zb .ctrl.zc .ctrl.zd grid .anim - - - -in .ctrl -row 100 -pady 5 grid .about - - - -in .ctrl -row 101 grid columnconfigure .ctrl {0 1 2 3} -weight 1 grid rowconfigure .ctrl 99 -weight 1 bind .c <Configure> {Recenter %W %h %w} bind all <F2> {console show} } proc Recenter {W h w} { set h [expr {$h / 2.0}] ; set w [expr {$w / 2.0}] $W config -scrollregion [list -$w -$h $w $h] DrawGrid Plotit } proc NewValue {args} { foreach who {a b c d} { set ::C(nice,$who) [format %.1f $::C($who)] } Plotit } proc DrawGrid {} { global S CLR .c delete all foreach {x0 y0 x1 y1} [.c cget -scrollregion] break set fnt {Times 8} for {set x 1} {1} {incr x} { set cx [expr {$x * $S(X)}] ;# Scaled to canvas if {$cx > $x1} break .c create line $cx $y0 $cx $y1 -fill white .c create line -$cx $y0 -$cx $y1 -fill white set n [.c create text $cx 0 -text $x -fill white -anchor n -font $fnt] .c create rect [.c bbox $n] -fill $S(bg) -outline $S(bg) .c raise $n set n [.c create text -$cx 0 -text -$x -fill white -anchor n -font $fnt] .c create rect [.c bbox $n] -fill $S(bg) -outline $S(bg) .c raise $n } for {set y 5} {1} {incr y 5} { set cy [expr {$y * $S(Y)}] ;# Scaled to canvas if {$cy > $y1} break .c create line $x0 $cy $x1 $cy -fill white .c create line $x0 -$cy $x1 -$cy -fill white set n [.c create text -3 $cy -text -$y -fill white -anchor e -font $fnt] .c create rect [.c bbox $n] -fill $S(bg) -outline $S(bg) .c raise $n set n [.c create text -3 -$cy -text $y -fill white -anchor e -font $fnt] .c create rect [.c bbox $n] -fill $S(bg) -outline $S(bg) .c raise $n } .c create line $x0 0 $x1 0 -fill blue .c create line 0 $y0 0 $y1 -fill blue .c create text [expr {$x0+20}] [expr {17.5*$S(Y)}] -tag equation \ -anchor w -font {Helvetica 10 bold italic} -fill $::S(eq) } proc Plotit {} { global C S .c delete plot foreach {x0 y0 x1 y1} [.c cget -scrollregion] break if {! [info exists x0]} return ;# Pre-update catch set xy {} for {set cx [expr {int($x0)}]} {$cx <= $x1} {incr cx} { set x [expr {$cx / double($S(X))}] set y [expr {$x * ($x * ($C(a)*$x + $C(b)) + $C(c)) + $C(d)}] set cy [expr {-1*$y * $S(Y)}] lappend xy $cx $cy } .c create line $xy -tag plot -fill red -width 2 .c itemconfig equation -text [GetEquation] } proc About {} { set msg "$::S(title)\nby Keith Vetter, December 2006\n\n" append msg "Visualization of the cubic equation" tk_messageBox -message $msg -title "About $::S(title)" } proc Zero {who} { set ::C($who) 0 NewValue } proc GetEquation {} { global C array set super {a x\u00b3 b x\u00b2 c x d ""} set txt "" foreach who {a b c d} { set num [format %.1f $C($who)] if {$num == 0} continue set num2 [expr {int($num) == $num ? abs(int($num)) : abs($num)}] if {$num2 == 1 && $who ne "d"} {set num2 ""} if {$num > 0} { if {$txt ne ""} { append txt " + "} } else { if {$txt eq ""} { append txt "-"} else {append txt " - "} } append txt $num2 $super($who) } if {$txt eq ""} {set txt 0} return "y = $txt" } if {[lsearch [image names] ::img::star] == -1} { image create bitmap ::img::star -data { #define plus_width 7 #define plus_height 7 static char plus_bits[] = { 0x49, 0x2a, 0x1c, 0x7f, 0x1c, 0x2a, 0x49} } } proc StartStop {} { set ::S(go) [expr {$::S(go) ? 0 : -1}] if {$::S(go)} Animate } proc Animate {{num ""}} { global S C MAX DIR if {$num ne ""} {set S(go) $num} foreach who {a b c d} { set next [expr {$C($who) + $DIR($who)}] if {abs($next) <= $MAX($who)} { set C($who) $next break } set DIR($who) [expr {-$DIR($who)}] } after idle NewValue if {$S(go) > 0} { incr S(go) -1 } if {$S(go)} { after $S(delay) Animate } } DoDisplay update NewValue after 200 Animate 20 return
UK you can find another implementation of this using BLT vector and graph in https://wiki.tcl-lang.org/15000 Example 3 ;-)
KPV don't know how I missed it :)
UK BLT is under appreciated, but for me it is still the first stop for rich plotting, vector math and tabsets.