Chebyshev approximation
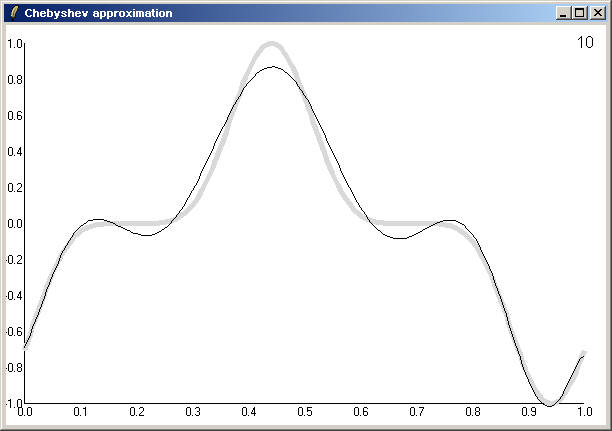
AM (15 july 2004) The code below illustrates graphically how approximating functions with Chebyshev polynomials works, it also forms a nice little package of mathematical methods. Implemented by kbk, put on the Wiki by me.
namespace eval ::math::approximate {
namespace export cheby_fit
}
#----------------------------------------------------------------------
#
# cheby_eval --
#
# Approximates a function with a truncated Chebyshev series
#
# Parameters:
# coef - List of coefficients of the Chebyshev polynomials
# a, b - Boundaries of the interval over which the Chebyshev
# fit was computed.
# x - Abscissa at which to evaluate the function
#
# Results:
# Returns an approximation to the function evaluated at x.
#
# Side effects:
# None.
#
#----------------------------------------------------------------------
proc ::math::approximate::cheby_eval { coef a b x } {
if { ( $x - $a ) * ( $x - $b ) > 1e-8 } {
return -code error "domain error: x not in interval"
}
set u [expr { ( $x + $x - $a - $b ) / ( $b - $a ) }]
set twou [expr { $u + $u }]
set v2 0.
set v1 0.
set j [llength $coef]
while { $j >= 2 } {
incr j -1
foreach { v2 v1 } \
[list $v1 [expr { $twou * $v1 - $v2 + [lindex $coef $j] }]] \
break
}
return [expr { $u * $v1 - $v2 + [lindex $coef 0] }]
}
#----------------------------------------------------------------------
#
# cheby_fit --
#
# Fits a function with a truncated Chebyshev series.
#
# Parameters:
# f - Function to fit, expressed as a command prefix to which
# the abscissa will be appended. The function is expected
# to return the ordinate.
# a,b - Interval over which to fit the function
# epsilon - Desired absolute error bound of the fit (approximate)
# n - Maximum order of the Chebyshev polynomial to include.
#
# Results:
# Returns a Tcl command prefix that, when evaluated with an
# abscissa postpended, will give an approximation to the function.
#
# Side effects:
# Evaluates the given function n times, so has whatever side
# effects it has. Also may cache a table of cosines.
#
#----------------------------------------------------------------------
proc ::math::approximate::cheby_fit { f a b {epsilon 1e-8} { n 50 } } {
set halfwidth [expr { ($b - $a) / 2. }]
set midpoint [expr { ( $b + $a ) / 2. }]
set cs [cos_table $n]
set c {}
for { set k 0 } { $k < $n } { incr k } {
lappend c 0.
}
set twon [expr { $n + $n }]
set fourn [expr { $twon + $twon }]
for { set k 1 } { $k <= $twon } { incr k 2 } {
set x [expr { [lindex $cs $k] * $halfwidth + $midpoint }]
set cmd $f; lappend cmd $x; set y [uplevel 1 $cmd]
set m 0
for { set j 0 } { $j < $n } { incr j } {
lset c $j [expr { [lindex $c $j] + $y * [lindex $cs $m] }]
incr m $k
if { $m >= $fourn } {
set m [expr { $m - $fourn }]
}
}
}
set r {}
foreach d $c {
lappend r [expr { $d * 2. / $n }]
}
lset r 0 [expr { [lindex $r 0] / 2. }]
for { set i [expr { $n-1 }] } { $i > 0 } { incr i -1 } {
if { abs([lindex $r $i]) > $epsilon } break
}
return [list [namespace which -command cheby_eval] [lrange $r 0 $i] $a $b]
}
#----------------------------------------------------------------------
#
# cos_table --
#
# Builds a cosine table for Chebyshev fitting.
#
# Parameters:
# n - Number of points.
#
# Results:
# Returns a list of length 4n. The ith element of the list
# is cos( i * pi / ( 2 * n ) )
#
# Side effects:
# Caches the cosine table.
#
#----------------------------------------------------------------------
proc ::math::approximate::cos_table { n } {
variable costable
if { [info exists costable($n)] } {
return $costable($n)
}
set theta [expr { 0.78539816339744828 / $n }]
set s [expr { sin($theta) }]
set alpha [expr { 2. * $s * $s }]
set beta [expr { sin( 2. * $theta ) }]
set c 1.
set s 0.
set table {}
for { set i 0 } { $i + $i <= $n } { incr i } {
lappend ctable $c
lappend stable $s
foreach { c s } \
[list \
[expr { $c - ( $alpha * $c + $beta * $s ) }] \
[expr { $s - ( $alpha * $s - $beta * $c ) }]] break
}
incr i [expr { ( $n % 2 ) - 1 }]
for { incr i -1 } { $i > 0 } { incr i -1 } {
lappend ctable [lindex $stable $i]
lappend stable [lindex $ctable $i]
}
foreach c $stable {
set c [expr {- $c}]
lappend ctable $c
}
foreach c $ctable {
set c [expr { - $c }]
lappend ctable $c
}
if { $n <= 100 } {
set costable($n) $ctable
}
return $ctable
}
if { ! [info exists ::argv0] || ![string equal [info script] $::argv0] } {
return
}
set tcl_precision 17
proc f { x } {
return [expr { pow( sin( 6.28318 * $x - 1.2 ), 5) }]
}
package require Tk
grid [canvas .c -width 600 -height 400 -bg white]
.c create line 20 20 20 380
.c create line 20 380 580 380
proc cx { x } {
expr { 560. * $x + 20. }
}
proc cy { y } {
expr { 200 - 180. * ( $y ) }
}
for { set xx 0 } { $xx <= 10 } { incr xx } {
set x [expr { $xx / 10. }]
.c create text [cx $x] 382 -anchor n -text [format %.1f $x]
}
for { set yy -10 } { $yy <= 10 } { incr yy 2 } {
set y [expr { $yy / 10. }]
.c create text 18 [cy $y] -anchor e -text [format %.1f $y]
}
set l {.c create line}
for { set x 0. } { $x < 1.0025 } { set x [expr { $x + 0.005 }] } {
set cmd f; lappend cmd $x; set y [eval $cmd]
lappend l [cx $x] [cy $y]
}
lappend l -width 5 -fill gray85
eval $l
.c create text 590 10 -anchor ne -tags n -font {Helvetica 12}
after 1000 set done 1; vwait done
set apx0 [::math::approximate::cheby_fit f 0. 1. 1.e-8 120]
for { set n 0 } { $n < [llength [lindex $apx0 1]] } { incr n } {
.c itemconfigure n -text $n
set apx $apx0
lset apx 1 [lrange [lindex $apx 1] 0 $n]
set l {.c create line}
set maxy2 0.
for { set x 0. } { $x < 1.0025 } { set x [expr { $x + 0.005 }] } {
set cmd $apx; lappend cmd $x; set y [eval $cmd]
lappend l [cx $x] [cy $y]
}
lappend l -tags apx
catch { .c delete apx }
eval $l
after 2000 set done 1; vwait done
}